题目内容
7．
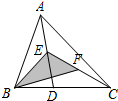如图，在△ABC中，已知点E、F分别是AD、CE边上的中点，且S△BEF=4cm2，则S△ABC的值为（ ）| A． | 1cm2 | B． | 2cm2 | C． | 8cm2 | D． | 16cm2 |
分析 由于E、F分别为BC、AD、CE的中点，可判断出BE、CE、BF为△ABD、△ACD、△BEC的中线，根据中线的性质可知将相应三角形分成面积相等的两部分，据此即可解答．
解答 解：∵由于E、F分别为AD、CE的中点，
∴△ABE、△DBE、△DCE、△AEC的面积相等，
∴S△BEC=2S△BEF=8（cm2），
∴S△ABC=2S△BEC=16（cm2）．
故选D．
点评 此题考查了三角形的面积，根据三角形中线将三角形的面积分成相等的两部分是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
17．在一次中学生田径运动会上，参加跳高的15名运动员的成绩如表：那么这些运动员跳高成绩的众数和中位数分别是（ ）
| 成绩（m） | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 2 | 4 | 3 | 3 | 2 |
| A． | 4和1.60 | B． | 1.75和1.65 | C． | 1.65和1.675 | D． | 1.65和1.70 |
15．若|x-y|+（y+1）2=0，则x2+y2的结果是（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 6 |
2．
如图，正方形ABCD的面积为4，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（ ）
如图，正方形ABCD的面积为4，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（ ）| A． | $\sqrt{8}$ | B． | 3 | C． | 4 | D． | 2 |
12．已知点D与点A（-5，0），B（0，12），C（a，a）是一平行四边形的四个顶点，则CD长的最小值为（ ）
| A． | 13 | B． | $\frac{13}{2}\sqrt{2}$ | C． | $\frac{17}{2}\sqrt{2}$ | D． | 12 |
