题目内容
6.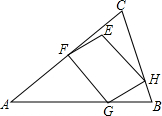 如图,在△ABC中,AB=AC,∠A=36°,?EFGH的顶点F、G、H分别在AC,AB,BC边上,且FC=CH.
如图,在△ABC中,AB=AC,∠A=36°,?EFGH的顶点F、G、H分别在AC,AB,BC边上,且FC=CH.(1)请仅用无刻度的直尺作出∠ACB的平分线.
(2)在(1)中,若∠ACB的平分线与AB交于点D,则下列关于点D的说法中正确的是( )
A.点D是AB的中点
B.点D是AB的一个黄金分割点
C.点D是AB的一个三等分点
D.AD:DB=3:2.
分析 (1)连接FH,EG,由?EFGH的对角线互相平分,得到点O是FH的中点,由三线合一得到CD是角的平分线;
(2)由等腰三角形的性质和角平分线的性质得到△CDB∽△ABC,列比例式求得AD=$\frac{\sqrt{5}-1}{2}$,得到点D是AB的一个黄金分割点.
解答 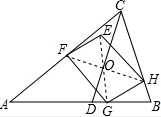 解:(1)如图连接EG,FH,交于点O,连接CO并延长交AB于D,
解:(1)如图连接EG,FH,交于点O,连接CO并延长交AB于D,
则AD即为所求;
(2)∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∵AD是∠ACB的平分线,
∴∠DCB=∠ACD=36°,
∴∠CDB=72°,
∴∠B=∠CDB,∠A=∠ACD,
∴CD=CB,AD=CD,
设BC=AD=CD=x,AC=AB=y,则BD=y-x,
∵△CDB∽△ABC,
∴$\frac{AC}{BC}$=$\frac{BC}{BD}$,∴$\frac{y}{x}$=$\frac{x}{y-x}$,
即:y2-xy-x2=0,
∴x=$\frac{\sqrt{5}-1}{2}$,
∴AD=$\frac{\sqrt{5}-1}{2}$,
∴点D是AB的一个黄金分割点.
故选B.
点评 本题考查了基本作图,等腰三角形的判定与性质,黄金分割,相似三角形的判定和性质,解题的关键是列比例式解得AD的长度后,能判断点D是黄金分割点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.在一次中学生田径运动会上,参加跳高的15名运动员的成绩如表:那么这些运动员跳高成绩的众数和中位数分别是( )
| 成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 2 | 4 | 3 | 3 | 2 |
| A. | 4和1.60 | B. | 1.75和1.65 | C. | 1.65和1.675 | D. | 1.65和1.70 |
14.将一枚质地均匀的硬币抛掷两次,则两次都是正面向上的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
11.下列各式中,最简二次根式是( )
| A. | $\sqrt{\frac{1}{x-y}}$ | B. | $\frac{a}{b}$ | C. | $\sqrt{{x}^{2}+4}$ | D. | $\sqrt{5{a}^{2}b}$ |
15.若|x-y|+(y+1)2=0,则x2+y2的结果是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
 如图,在菱形ABCD中,cosA=$\frac{3}{5}$,BE=2,则tan∠BDE=2.
如图,在菱形ABCD中,cosA=$\frac{3}{5}$,BE=2,则tan∠BDE=2.