题目内容
5.一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图方式拼接.若用餐的人数有90人,则这样的餐桌需要( )张?
| A. | 15 | B. | 16 | C. | 21 | D. | 22 |
分析 根据图形可知,每张桌子有4个座位,然后再加两端的各一个,于是n张桌子就有(4n+2)个座位;由此进一步列方程解答即可.
解答 解:1张长方形餐桌的四周可坐4+2=6人,
2张长方形餐桌的四周可坐4×2+2=10人,
3张长方形餐桌的四周可坐4×3+2=14人,
…
n张长方形餐桌的四周可坐4n+2人;
4n+2=90
解得n=22
答:这样的餐桌需要22张.
故选:D.
点评 此题考查图形的变化规律,首先应找出哪些部分发生了变化,是按照什么规律变化的,找出规律解决问题.

练习册系列答案
相关题目
15.若|x-y|+(y+1)2=0,则x2+y2的结果是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
20.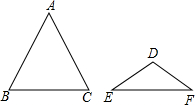 如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为( )
如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为( )
 如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为( )
如图,△ABC与△DEF都是等腰三角形,且AB=AC=3,DE=DF=2,若∠B+∠E=90°,则△ABC与△DEF的面积比为( )| A. | 9:4 | B. | 3:2 | C. | $\sqrt{3}:\sqrt{2}$ | D. | $3\sqrt{3}:2\sqrt{2}$ |
10.已知0≤x≤$\frac{3}{2}$,则函数y=x2+x+1( )
| A. | 有最小值$\frac{3}{4}$,但无最大值 | B. | 有最小值$\frac{3}{4}$,有最大值1 | ||
| C. | 有最小值1,有最大值$\frac{19}{4}$ | D. | 无最小值,也无最大值 |
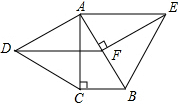 如图,分别以Rt△ABC的直角边AC和斜边AB向外作等边△ACD、等边△ABE,已知∠BAC=30°,BC=1,EF⊥AB,垂足为F,连结DF.
如图,分别以Rt△ABC的直角边AC和斜边AB向外作等边△ACD、等边△ABE,已知∠BAC=30°,BC=1,EF⊥AB,垂足为F,连结DF.