题目内容
已知抛物线y=x2-4x+3
(1)求该抛物线与x轴的交点坐标;
(2)当x取何值时,y>0?
(1)求该抛物线与x轴的交点坐标;
(2)当x取何值时,y>0?
考点:抛物线与x轴的交点
专题:
分析:(1)将抛物线解析式转化为两点式方程,可以直接写出答案;
(2)根据抛物线的性质解答.
(2)根据抛物线的性质解答.
解答:解:(1)∵y=x2-4x+3=(x-1)(x-3),
∴该抛物线与x轴的交点坐标是(1,0)和(3,0);
(2)由(1)知,该抛物线与x轴的交点坐标是(1,0)和(3,0).
∵y=x2-4x+3=(x-2)2-1,
∴该抛物线的顶点坐标是(2,-1),且抛物线的开口方向向上,大致图象如图所示:

∴当x<1或x>3时,y>0.
∴该抛物线与x轴的交点坐标是(1,0)和(3,0);
(2)由(1)知,该抛物线与x轴的交点坐标是(1,0)和(3,0).
∵y=x2-4x+3=(x-2)2-1,
∴该抛物线的顶点坐标是(2,-1),且抛物线的开口方向向上,大致图象如图所示:

∴当x<1或x>3时,y>0.
点评:此题主要考查抛物线的基本性质,解题的关键是应用因分解法求方程的根,把函数的方程结合起来出题,是一种比较好的题型.

练习册系列答案
相关题目
一个直角三角形的三边长为三个连续的整数,则斜边长为( )
| A、4 | B、5 | C、8 | D、10 |
若正多边形面积是100,周长是40,则它的边心距是( )
| A、5 | B、2.5 | C、10 | D、20 |
 如图,圆内接四边形ABCD,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,求∠A的度数.
如图,圆内接四边形ABCD,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,求∠A的度数. 在如图的三张纸片中,能够折叠成三棱锥的是
在如图的三张纸片中,能够折叠成三棱锥的是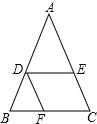 如图所示,已知DE∥BC,DF∥AC,且AE=3,AC=5,BC=10,求BF的长.
如图所示,已知DE∥BC,DF∥AC,且AE=3,AC=5,BC=10,求BF的长.