题目内容
2.已知直线L2:y=-3x+24,直线L1:y=$\frac{1}{2}$x+3,交于点C,直线L1和直线L2分别交x轴于B、A,过点A作AD⊥x轴并交L1于D,过点D作DE∥x轴并交L2于E,再过E作x轴垂线,垂足为F,得到矩形GDEF(G与A重合)(1)求△ABC的面积;
(2)求矩形GDEF的边DE和EF的长;
(3)若将矩形GDEF沿x轴的负方向以每秒一个单位长度的速度平移,设移动时间为t(s)(0≤t≤14),求矩形GDEF平移过程中,矩形GDEF与△ABC公共部分的面积S与矩形运动时间t(秒)之间的函数关系,并写出相应的t的范围.
分析 (1)将y=0分别代入两直线解析式,即可得出A、B点的坐标,令-3x+24=$\frac{1}{2}$x+3,解方程可得出C点的横坐标,将其代入直线解析式中即可得出C点的纵坐标,结合三角形的面积公式即可得出结论;
(2)依照题意画出图形,将x=8代入直线L1中解出D点横坐标,由此能得出D点的坐标;再将D点的纵坐标代入直线L2中可求得E点的横坐标,由此可得出点E的坐标;由EF⊥x轴即可得出F点的坐标,结合点的坐标即可求出DE和EF的长;
(3)由DE=$\frac{7}{3}$>2,可知整个运动过程可以分三部分讨论,根据直线的斜率可得出分割图形,结合三角形和梯形的面积公式即可得出结论.
解答 解:(1)令y=0,则有-3x+24=0和$\frac{1}{2}$x+3=0,
解得:x=8和x=-6,
∴点B的坐标为(-6,0),点A的坐标为(8,0).
令-3x+24=$\frac{1}{2}$x+3,解得:x=6,
此时y=$\frac{1}{2}$×6+3=6,即点C的坐标为(6,6).
∴△ABC的面积S△ABC=$\frac{1}{2}$×[8-(-6)]×6=42.
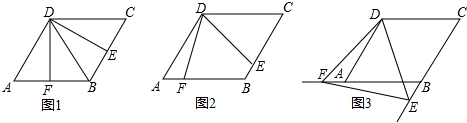
(2)依照题意画出图形,如图1所示.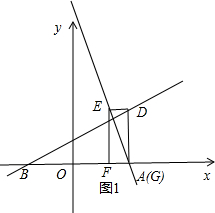
将x=8代入直线L1:y=$\frac{1}{2}$x+3中,
得:y=$\frac{1}{2}$×8+3=7,
即点D的坐标为(8,7);
将y=7代入直线L2:y=-3x+24,
则有7=-3x+24,解得:x=$\frac{17}{3}$,
即点E的坐标为($\frac{17}{3}$,7);
又∵EF⊥x轴,
∴点F的坐标为($\frac{17}{3}$,0).
∴DE=8-$\frac{17}{3}$=$\frac{7}{3}$,EF=7-0=7.
(3)随着矩形的运动,分三种情况:
①点C在线段DG的左侧,如图2所示.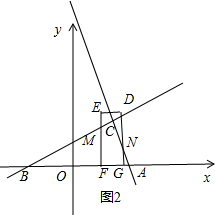
此时0≤AG<8-6,即0≤t<2.
AG=t,NG=3AG=3t,BF=AB-FG-AG=14-$\frac{7}{3}$-t=$\frac{35}{3}$-t,MF=$\frac{1}{2}$BF=$\frac{35}{6}$-$\frac{t}{2}$.
此时S=S△ABC-S△BFM-S△AGN=42-$\frac{1}{2}$BF•MF-$\frac{1}{2}$AG•NG=-$\frac{7}{4}{t}^{2}$+$\frac{35}{6}$t+$\frac{287}{36}$;
②点C在线段DG的右侧(或在线段DG上),点B在线段EF的左侧(或在线段EF上),由图3所示.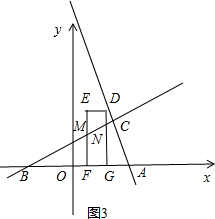
此时8-6≤AG≤AB-FG,即2≤t≤$\frac{35}{3}$,
AG=t,BG=AB-AG=14-t,NG=$\frac{1}{2}$BG=7-$\frac{1}{2}$t,BF=AB-AG-FG=$\frac{35}{3}$-t,MF=$\frac{1}{2}$BF=$\frac{35}{6}$-$\frac{1}{2}$t.
此时S=$\frac{1}{2}$(MF+NG)•FG=$\frac{1}{2}$×($\frac{35}{6}$-$\frac{1}{2}$t+7-$\frac{1}{2}$t)×$\frac{7}{3}$=-$\frac{7}{6}$t+$\frac{539}{36}$;
③点B在EF的右边,点B在线段DG的左侧(或在线段DG上),如图4所示.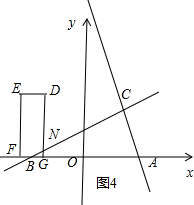
此时AB-FG<AG≤AB,即$\frac{35}{3}$<t≤14,
AG=t,BG=AB-AG=14-t,NG=$\frac{1}{2}$BG=7-$\frac{1}{2}$t.
此时S=$\frac{1}{2}$BG•NG=$\frac{1}{2}$×(14-t)×(7-$\frac{1}{2}$t)=$\frac{1}{4}{t}^{2}$-7t+49.
综上可知:矩形GDEF与△ABC公共部分的面积S=$\left\{\begin{array}{l}{-\frac{7}{4}{t}^{2}+\frac{35}{6}t+\frac{287}{36}(0≤t<2)}\\{-\frac{7}{6}t+\frac{539}{36}(2≤t≤\frac{35}{3})}\\{\frac{1}{4}{t}^{2}-7t+49(\frac{35}{3}<t≤14)}\end{array}\right.$.
点评 本题考查了一次函数的应用、三角形的面积公式、梯形的面积公式以及解一元一次方程,解题的关键是:(1)求出A、B、C三点的坐标;(2)求出D、E、F三点的坐标;(3)依照运动过程分段考虑.本题属于中档题,(1)(2)难度不大;(3)利用矩形运动过程中图形的不同分三部分考虑,期间用到了分割图形求面积,分割法是我们中学阶段常用到的求面积的手段,在日常学习中应加强练习.

 优学名师名题系列答案
优学名师名题系列答案 可记为an,如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3)
可记为an,如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3)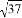 最接近的数是()
最接近的数是()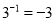 B.
B. 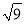 = ±3 C. (ab2)3= a3b6 D. a6÷a2 = a3
= ±3 C. (ab2)3= a3b6 D. a6÷a2 = a3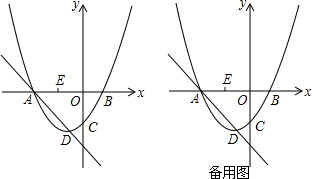
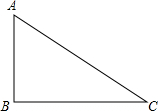 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.