题目内容
13.已知a,b,c是△ABC的三边,试说明:(a2+b2-c2)2-4a2b2的值一定是负数.分析 原式利用平方差公式分解,再利用完全平方公式变形,继续利用平方差公式分解,利用两边之和大于第三边,两边之差小于第三边,即可确定出正负.
解答 解:(a2+b2-c2)2-4a2b2
=(a2+b2-c2+2ab)(a2+b2-c2-2ab)
=[(a+b)2-c2][(a-b)2-c2]
=(a+b+c)(a+b-c)(a-b-c)(a-b+c),
∵a,b,c是三角形ABC三边,
∴a+b+c>0,a+b-c>0,a-b-c<0,a-b+c>0,
∴(a+b+c)(a+b-c)(a-b-c)(a-b+c)<0,即值为负数.
点评 此题考查了因式分解的应用,以及三角形的三边关系,将已知式子进行适当的变形是解本题的关键.

练习册系列答案
相关题目
3.下列关于一元二次方程的根判断,说法一定正确的是( )
| A. | 方程x2-x+1=0的两实数根之和等于-1 | |
| B. | 方程x2+x+1=0的两实数根之积等于1 | |
| C. | 方程x2-x-1=0的两实数根之和等于1 | |
| D. | 方程x2+x-1=0的两实数根之积等于1 |
8.某班运来一筐苹果,若每人分6个则少6个;若每人分5个则多5个,那么该班人数与苹果数分别是( )
| A. | 22,120 | B. | 11,60 | C. | 10,54 | D. | 8,42 |
18.若分式1-$\frac{3}{x+2}$的值为0,则x的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
2.反比例函数y=-$\frac{12}{x}$的图象不经过点( )
| A. | (4,3) | B. | (2,-6) | C. | (1,-12) | D. | (-6,2) |
3.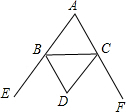 如图,△ABC的外角∠CBE,∠BCF的平分线BD,CD相交于点D,设∠BDC=α,那么∠A=( )
如图,△ABC的外角∠CBE,∠BCF的平分线BD,CD相交于点D,设∠BDC=α,那么∠A=( )
 如图,△ABC的外角∠CBE,∠BCF的平分线BD,CD相交于点D,设∠BDC=α,那么∠A=( )
如图,△ABC的外角∠CBE,∠BCF的平分线BD,CD相交于点D,设∠BDC=α,那么∠A=( )| A. | 90°-α | B. | 90°-$\frac{1}{2}$α | C. | 180°-$\frac{1}{2}$α | D. | 180°-2α |
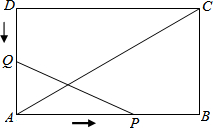 如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t(s)表示运动时间(0≤t≤6).
如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t(s)表示运动时间(0≤t≤6).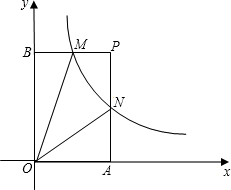 如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OAPB边PB中点M,交PA与点N,且四边形ONPM的面积为$\frac{3}{2}$,则k的值为$\frac{3}{2}$.
如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OAPB边PB中点M,交PA与点N,且四边形ONPM的面积为$\frac{3}{2}$,则k的值为$\frac{3}{2}$.