题目内容
5.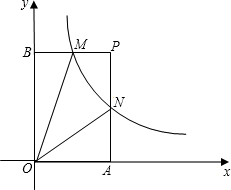 如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OAPB边PB中点M,交PA与点N,且四边形ONPM的面积为$\frac{3}{2}$,则k的值为$\frac{3}{2}$.
如图,已知双曲线y=$\frac{k}{x}$(x>0)经过矩形OAPB边PB中点M,交PA与点N,且四边形ONPM的面积为$\frac{3}{2}$,则k的值为$\frac{3}{2}$.
分析 设M(a,$\frac{k}{a}$),由于M为PB的中点,则P(2a,$\frac{k}{a}$),根据反比例函数的比例系数k的几何意义得S△OBM=S△OAN=$\frac{1}{2}$k,则利用S四边形ONPM=S矩形APBO-S△OBM-S△OAN得2a•$\frac{k}{a}$-$\frac{1}{2}$k-$\frac{1}{2}$k=$\frac{3}{2}$,然后解k的方程即可.
解答 解:设M(a,$\frac{k}{a}$),则P(2a,$\frac{k}{a}$),
∵S四边形ONPM=S矩形APBO-S△OBM-S△OAN,
而S△OBM=S△OAN=$\frac{1}{2}$k,
∴2a•$\frac{k}{a}$-$\frac{1}{2}$k-$\frac{1}{2}$k=$\frac{3}{2}$,
∴k=$\frac{3}{2}$.
故答案为$\frac{3}{2}$.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
相关题目
15.长度单位1纳米=10-9米,一种新型病毒直径为3100纳米,用科学记数法表示该病毒直径是( )米.
| A. | 31×10-6 | B. | 0.31×10-5 | C. | 3.1×10-6 | D. | 3.1×10-5 |
20. 如图,∠BAC=∠DCA,∠B=72°,则∠BCD的度数为( )
如图,∠BAC=∠DCA,∠B=72°,则∠BCD的度数为( )
 如图,∠BAC=∠DCA,∠B=72°,则∠BCD的度数为( )
如图,∠BAC=∠DCA,∠B=72°,则∠BCD的度数为( )| A. | 70° | B. | 72° | C. | 100° | D. | 108° |
10.下列运算正确的是( )
| A. | (-4m2)3=-4m6 | B. | ${(-\frac{1}{2})^{-4}}+{(π-3)^0}$=16 | ||
| C. | (a+b)2=(a-b)2+4ab | D. | $9{x^3}{y^2}÷(-\frac{1}{3}{x^3}y)=-3y$ |
 如图,已知:B、F、C、E在一条直线上,FB=CE,AC=DF,能否由上面的已知条件,添加到已知条件中,使AB∥ED成立,并给出证明供选择的三个条件(请从其中选择一个):
如图,已知:B、F、C、E在一条直线上,FB=CE,AC=DF,能否由上面的已知条件,添加到已知条件中,使AB∥ED成立,并给出证明供选择的三个条件(请从其中选择一个):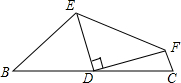 如图,四边形BEFC中D为BC的中点,∠EDF=90°,求证:BE+FC>EF.
如图,四边形BEFC中D为BC的中点,∠EDF=90°,求证:BE+FC>EF.