题目内容
3.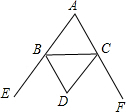 如图,△ABC的外角∠CBE,∠BCF的平分线BD,CD相交于点D,设∠BDC=α,那么∠A=( )
如图,△ABC的外角∠CBE,∠BCF的平分线BD,CD相交于点D,设∠BDC=α,那么∠A=( )| A. | 90°-α | B. | 90°-$\frac{1}{2}$α | C. | 180°-$\frac{1}{2}$α | D. | 180°-2α |
分析 根据三角形的一个外角等于和它不相邻的两个内角的和、角平分线的定义以及三角形的内角和定理即可解答.
解答 解:α=180°-(∠DBC+∠DCB)
=180°-$\frac{1}{2}$(∠CBE+∠BCF)
=180°-$\frac{1}{2}$(∠A+∠ACB+∠BCF)
=180°-$\frac{1}{2}$(180°+∠A)
=90°-$\frac{1}{2}$∠A.
则∠A=180°-2α.
故选D.
点评 本题考查的是三角形外角的性质及三角形内角和定理:
(1)三角形外角的性质:三角形的外角等于和它不相邻的两个内角的和;
(2)三角形内角和定理:三角形的内角和为180°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.一元二次方程3x2-4x=5的二次项系数是( )
| A. | 3 | B. | -4 | C. | 5 | D. | -5 |
13.下列叙述的运动属于旋转的是( )
| A. | 运动员在100米跑道上赛跑 | B. | 竖直下落的石子 | ||
| C. | 电风扇启动后,它的叶子的运动 | D. | 静止的车轮 |
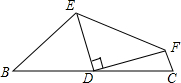 如图,四边形BEFC中D为BC的中点,∠EDF=90°,求证:BE+FC>EF.
如图,四边形BEFC中D为BC的中点,∠EDF=90°,求证:BE+FC>EF.