题目内容
(10分) 如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.

 360°.
【解析】试题分析:连接BE,根据三角形外角的性质可得∠1=∠C+∠D=∠CBE+∠DEB,再由四边形的内角和定理可得∠A+∠ABC+∠C+∠D+∠DEF+∠F=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F=∠A+∠ABE+∠BEF+∠F=360°.
试题解析:【解析】
如图,连接BE.
∵∠1=∠C+∠D,∠1=∠CBE+∠DEB,
∴∠C+∠D=∠CB...
360°.
【解析】试题分析:连接BE,根据三角形外角的性质可得∠1=∠C+∠D=∠CBE+∠DEB,再由四边形的内角和定理可得∠A+∠ABC+∠C+∠D+∠DEF+∠F=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F=∠A+∠ABE+∠BEF+∠F=360°.
试题解析:【解析】
如图,连接BE.
∵∠1=∠C+∠D,∠1=∠CBE+∠DEB,
∴∠C+∠D=∠CB...
练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
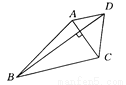
如图所示,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=5 ㎝, BD=12 ㎝,则该梯形的两底之和等于____㎝.
 13
【解析】【解析】
过点D作DE∥AC交BC的延长线于E,则DE与AC平行且相等,AD=CE.∵AC⊥BD,∴BD⊥DE.在Rt△BDE中,BE==13,∴BC+AD=13.
13
【解析】【解析】
过点D作DE∥AC交BC的延长线于E,则DE与AC平行且相等,AD=CE.∵AC⊥BD,∴BD⊥DE.在Rt△BDE中,BE==13,∴BC+AD=13. 为了更好地保护美丽如画的邛海湿地,西昌市污水处理厂决定先购买A,B两种型号的污水处理设备共20台,对邛海湿地周边污水进行处理.每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640 t,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1 080 t.
(1)求A,B两种型号的污水处理设备每周每台分别可以处理污水多少吨.
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4 500 t,请你列举出所有购买方案,并指出哪种方案所需资金最少,最少是多少.
 (1) A型污水处理设备每周每台可以处理污水240 t,B型污水处理设备每周每台可以处理污水200 t(2)购买A型污水处理设备13台,购买B型污水处理设备7台时,所需资金最少,最少是226万元
【解析】(1)根据1台A型污水处理设备+2台B型污水处理设备=每周可以处理污水640吨,2台A型污水处理设备+3台B型污水处理设备=每周可以处理污水1080吨,关系式列出二元一次方程组,从而解答即可...
(1) A型污水处理设备每周每台可以处理污水240 t,B型污水处理设备每周每台可以处理污水200 t(2)购买A型污水处理设备13台,购买B型污水处理设备7台时,所需资金最少,最少是226万元
【解析】(1)根据1台A型污水处理设备+2台B型污水处理设备=每周可以处理污水640吨,2台A型污水处理设备+3台B型污水处理设备=每周可以处理污水1080吨,关系式列出二元一次方程组,从而解答即可... 下列各项中,不是不等式x≤2解的是( )
A. 0 B. 2 C. 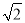 D.
D. 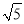
 D
【解析】由于>2,所以不是x≤2的解.
故选:D.
D
【解析】由于>2,所以不是x≤2的解.
故选:D. 过n边形的一个顶点有7条对角线,m边形有m条对角线,p边形没有对角线,q边形的内角和与外角和相等,求q(n-m)p的值.
 500
【解析】分析:若过n边形的一个顶点有7条对角线,则n=10;m边形有m条对角线,即得到方程m(m-3)=m,解得m=5;P边形没有对角线,只有三角形没有对角线,因而P=3;q边形的内角和与外角和相等,内角和与外角和相等的只有四边形,因而q=4.代入代数式就可以求出代数式的值.
本题解析:
∵n边形从一个顶点发出的对角线有n-3条,∴n=7+3=10,
∵m边形有...
500
【解析】分析:若过n边形的一个顶点有7条对角线,则n=10;m边形有m条对角线,即得到方程m(m-3)=m,解得m=5;P边形没有对角线,只有三角形没有对角线,因而P=3;q边形的内角和与外角和相等,内角和与外角和相等的只有四边形,因而q=4.代入代数式就可以求出代数式的值.
本题解析:
∵n边形从一个顶点发出的对角线有n-3条,∴n=7+3=10,
∵m边形有... 若一个三角形的三边长分别为3 m,4 m,5 m,那么这个三角形的面积为___.
 6 m2
【解析】根据勾股定理的逆定理,可由三边的长判断出此三角形是直角三角形,3cm、4cm是三角形的两直角边,所以根据三角形的面积公式可得面积为3×4÷2=6m2.
故答案为:6m2.
6 m2
【解析】根据勾股定理的逆定理,可由三边的长判断出此三角形是直角三角形,3cm、4cm是三角形的两直角边,所以根据三角形的面积公式可得面积为3×4÷2=6m2.
故答案为:6m2. 如图,在△ABC中,AC=4 cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7 cm,则BC的长为( )
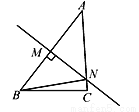
A. 1 cm B. 2 cm C. 3 cm D. 4 cm
 C
【解析】试题分析:根据中垂线的性质可得:BN=AN,则△BCN的周长=BN+NC+BC=AN+NC+BC=AC+BC=7cm,根据AC=4cm可得:BC=7-4=3cm.
C
【解析】试题分析:根据中垂线的性质可得:BN=AN,则△BCN的周长=BN+NC+BC=AN+NC+BC=AC+BC=7cm,根据AC=4cm可得:BC=7-4=3cm. 计算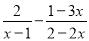 的结果是____________.
的结果是____________.
 【解析】 本题考查的是分式的加减
先通分,再把分子部分相加减,分母不变。
原式.
【解析】 本题考查的是分式的加减
先通分,再把分子部分相加减,分母不变。
原式. 已知?ABCD的周长为32,AB=4,则BC=( )
A. 4 B. 12 C. 24 D. 28
 B
【解析】【解析】
由题意得,,AB=4,解得BC=12,故选B。
B
【解析】【解析】
由题意得,,AB=4,解得BC=12,故选B。 
