题目内容
13.若点O为?ABCD的对角线AC与BD交点,且AO+BO=13cm,则AC+BD=26cm.分析 利用平行四边形的性质得出对角线互相平分,进而得出答案.
解答 解:∵四边形ABCD是平行四边形,点O为?ABCD的对角线AC与BD交点,
∴AO=BO,CO=DO,
∵AO+BO=13cm,
∴AC+BD=26cm.
故答案为:26cm.
点评 此题主要考查了平行四边形的性质,得出其对角线互相平分是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.在?ABCD中,对角线AC和BD相交于点O,如果AC=24,BD=20,AB=m,则m的取值范围是( )
| A. | 20<m<24 | B. | 4<m<44 | C. | 2<m<22 | D. | 10<m<12 |
5.下列分式一定有意义的是( )
| A. | $\frac{{x}^{2}+1}{{x}^{2}-1}$ | B. | $\frac{x+1}{{x}^{2}}$ | C. | $\frac{x-1}{{x}^{2}+1}$ | D. | $\frac{{x}^{2}}{x+1}$ |
2. 已知OA,OB是⊙O的半径,点C在⊙O上,∠OBA=50°,则∠C的度数为( )
已知OA,OB是⊙O的半径,点C在⊙O上,∠OBA=50°,则∠C的度数为( )
 已知OA,OB是⊙O的半径,点C在⊙O上,∠OBA=50°,则∠C的度数为( )
已知OA,OB是⊙O的半径,点C在⊙O上,∠OBA=50°,则∠C的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 80° |
3.小明有两根3cm、7cm的木棒,他想以这两根木棒为边做一个三角形,还需再选用的木棒长为( )
| A. | 3cm | B. | 4cm | C. | 9cm | D. | 10cm |
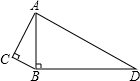 如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,求AD的长.
如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,求AD的长.