题目内容
3.已知:a-b=$\sqrt{3}$+$\sqrt{2}$,b-c=$\sqrt{3}$-$\sqrt{2}$,求a2+b2+c2-ab-ac-ab的值.分析 根据a-b=$\sqrt{3}$+$\sqrt{2}$,b-c=$\sqrt{3}$-$\sqrt{2}$,可得a-c=2$\sqrt{3}$,先计算2(a2+b2+c2-ab-ac-ab)的值,再除以2即可.
解答 解:∵a-b=$\sqrt{3}$+$\sqrt{2}$,b-c=$\sqrt{3}$-$\sqrt{2}$,
∴a-c=2$\sqrt{3}$,
∵2(a2+b2+c2-ab-ac-ab)=(a-b)2+(b-c)2+(a-c)2
=($\sqrt{3}$+$\sqrt{2}$)2+($\sqrt{3}$-$\sqrt{2}$)2+(2$\sqrt{3}$)2
=5+2$\sqrt{6}$+5-2$\sqrt{6}$+12
=22,
∴a2+b2+c2-ab-ac-ab=11.
点评 本题考查了二次根式的化简求值以及因式分解的应用,要熟练掌握添项和拆项,凑完全平方公式是解题的关键

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
8.如图,甲、乙、丙三个图形都是由大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数.其中主视图相同的是( )
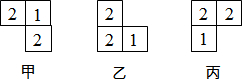
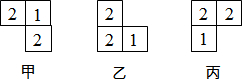
| A. | 仅有甲和乙相同 | B. | 仅有甲和丙相同 | C. | 仅有乙和丙相同 | D. | 甲、乙、丙都相同 |
 如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于60度.
如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于60度.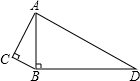 如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,求AD的长.
如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,求AD的长.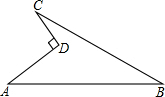 如图所示的一块地,AD=9m,CD=12m,∠ADC=90°,AB=39m,BC=36m,求这块地的面积.
如图所示的一块地,AD=9m,CD=12m,∠ADC=90°,AB=39m,BC=36m,求这块地的面积. 附加题
附加题