题目内容
4.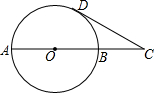 已知,AB是⊙O的一条直径,延长AB至C点,使AC=3BC,CD与⊙O相切于D点,若CD=$\sqrt{3}$,则⊙O半径的长为1.
已知,AB是⊙O的一条直径,延长AB至C点,使AC=3BC,CD与⊙O相切于D点,若CD=$\sqrt{3}$,则⊙O半径的长为1.
分析 如图,连接DO,首先根据切线的性质可以得到∠ODC=90°,又AC=3BC,O为AB的中点,由此可以得到∠C=30°,利用锐角三角函数的定义可得OD=$\frac{\sqrt{3}}{3}$CD,可得结果.
解答 解:如图,连接DO,
∵CD是⊙O切线,
∴OD⊥CD,
∴∠ODC=90°,
∵AB是⊙O的一条直径,AC=3BC,
∴AB=2BC=OC=2OD,
∴∠C=30°,
∴OD=$\frac{\sqrt{3}}{3}$CD,
∵CD=$\sqrt{3}$,
∴OD=BC=1.
故答案为:1.
点评 本题考查了圆的切线性质及解直角三角形的知识,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题是解答本题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
14.将9+(-3)-(-7)+(-2.5)写成省略加号的和的形式为( )
| A. | -9-3+7-2.5 | B. | 9-3-7-2.5 | C. | 9-3+7-2.5 | D. | 9+3-7-2.5 |
15.$-1\frac{1}{4}$倒数的相反数是( )
| A. | $\frac{5}{4}$ | B. | -1$\frac{1}{4}$ | C. | $-\frac{4}{5}$ | D. | $\frac{4}{5}$ |
9.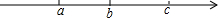 在数轴上表示有理数a,b,c的点如图所示,若ac<0,b+a<0,则( )
在数轴上表示有理数a,b,c的点如图所示,若ac<0,b+a<0,则( )
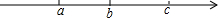 在数轴上表示有理数a,b,c的点如图所示,若ac<0,b+a<0,则( )
在数轴上表示有理数a,b,c的点如图所示,若ac<0,b+a<0,则( )| A. | b+c<0 | B. | |b|<|c| | C. | |a|>|b| | D. | abc<0 |
 如图,为了测量某电线杆(底部可到达)的高度,准备了如下的测量工具:
如图,为了测量某电线杆(底部可到达)的高度,准备了如下的测量工具:
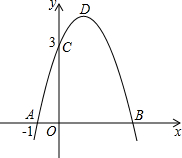 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为A(-1,0),另一交点为B,与y轴的交点坐标为C(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为A(-1,0),另一交点为B,与y轴的交点坐标为C(0,3).