题目内容
19.方程$x+\frac{x}{1+2}+\frac{x}{1+2+3}+…+\frac{x}{1+2+…+2015}=2015$的解是x=1008.分析 方程左边整理后,利用拆项法变形,计算即可求出解.
解答 解:方程整理得:x($\frac{2}{1×2}$+$\frac{2}{2×3}$+$\frac{2}{3×4}$+…+$\frac{2}{2015×2016}$)=2015,
即2x(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2015}$-$\frac{1}{2016}$)=2015,
化简得:2x(1-$\frac{1}{2016}$)=2015,即2x•$\frac{2015}{2016}$=2015,
整理得:2x=2016,
解得:x=1008.
故答案为:1008.
点评 此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
10.下列图形中不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.点M在x轴的上方,距离x轴4个单位长度,距离y轴3个单位长度,则M点的坐标为( )
| A. | (4,3) | B. | (3,4) | C. | (-4,3)或(4,3) | D. | (-3,4)或(3,4) |
14.已知a2+bc=14,b2-2bc=-6,则3a2+4b2-5bc的值是( )
| A. | 8 | B. | 12 | C. | 16 | D. | 18 |
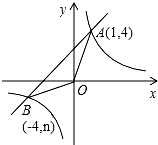 已知:如图,反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=x+b的图象交于点A(1,4),点B(-4,n).
已知:如图,反比例函数y1=$\frac{k}{x}$的图象与一次函数y2=x+b的图象交于点A(1,4),点B(-4,n).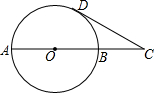 已知,AB是⊙O的一条直径,延长AB至C点,使AC=3BC,CD与⊙O相切于D点,若CD=$\sqrt{3}$,则⊙O半径的长为1.
已知,AB是⊙O的一条直径,延长AB至C点,使AC=3BC,CD与⊙O相切于D点,若CD=$\sqrt{3}$,则⊙O半径的长为1. 如图所示,点A在线段CB上,AC=$\frac{1}{2}AB$,点D是线段BC的中点.若CD=3,求线段AD的长.
如图所示,点A在线段CB上,AC=$\frac{1}{2}AB$,点D是线段BC的中点.若CD=3,求线段AD的长.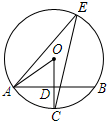 如图,AB是⊙O的一条弦,且AB=$4\sqrt{3}$.点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.
如图,AB是⊙O的一条弦,且AB=$4\sqrt{3}$.点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.