题目内容
12.计算(1)$\frac{{a}^{2}}{a+b}$+$\frac{{b}^{2}+2ab}{a+b}$
(2)$(\frac{3y}{y-3}-\frac{y}{y+3})•\frac{{{y^2}-9}}{y}$
(3)化简代数式 $\frac{{{x^2}-1}}{{{x^2}+2x}}÷\frac{x-1}{x}$,并判断当x满足不等式组 $\left\{\begin{array}{l}{x+2<1}\\{2(x-1)>-6}\end{array}\right.$时该代数式的符号.
分析 (1)根据同分母分式相加的方法进行计算即可;
(2)先将括号内的分式通分,然后在化简即可;
(3)先对题目中的分式化简,再求出不等式组的解集,然后讨论化简后的分式的正负情况,即可解答本题.
解答 解:(1)$\frac{{a}^{2}}{a+b}$+$\frac{{b}^{2}+2ab}{a+b}$
=$\frac{{a}^{2}+{b}^{2}+2ab}{a+b}$
=$\frac{(a+b)^{2}}{a+b}$
=a+b;
(2)$(\frac{3y}{y-3}-\frac{y}{y+3})•\frac{{{y^2}-9}}{y}$
=$\frac{3y(y+3)-y(y-3)}{(y-3)(y+3)}•\frac{(y+3)(y-3)}{y}$
=3(y+3)-(y-3)
=3y+9-y+3
=2y+12;
(3)$\frac{{{x^2}-1}}{{{x^2}+2x}}÷\frac{x-1}{x}$
=$\frac{(x+1)(x-1)}{x(x+2)}×\frac{x}{x-1}$
=$\frac{x+1}{x+2}$,
解 $\left\{\begin{array}{l}{x+2<1}\\{2(x-1)>-6}\end{array}\right.$,得-2<x<-1,
当-2<x<-1时,x+1<0,x+2>0,故$\frac{x+1}{x+2}<0$,
即当x满足不等式组 $\left\{\begin{array}{l}{x+2<1}\\{2(x-1)>-6}\end{array}\right.$时该代数式的符号为负号.
点评 本题考查分式的混合运算、解一元一次不等式,解题的关键是明确分式的加减乘除的计算方法和如何解答一元一次不等式组.

练习册系列答案
相关题目
2.据某市统计局公布的数据,今年一季度该市实现国民生产总值约为14800000000元.14800000000元用科学记数法表示为( )
| A. | 1.48×1011 | B. | 1.48×1010 | C. | 0.148×1011 | D. | 14.8×109 |
7.点M在x轴的上方,距离x轴4个单位长度,距离y轴3个单位长度,则M点的坐标为( )
| A. | (4,3) | B. | (3,4) | C. | (-4,3)或(4,3) | D. | (-3,4)或(3,4) |
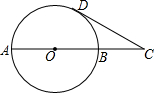 已知,AB是⊙O的一条直径,延长AB至C点,使AC=3BC,CD与⊙O相切于D点,若CD=$\sqrt{3}$,则⊙O半径的长为1.
已知,AB是⊙O的一条直径,延长AB至C点,使AC=3BC,CD与⊙O相切于D点,若CD=$\sqrt{3}$,则⊙O半径的长为1.