题目内容
9.同学们,今天我们来学习一个新知识.这是一个高中或者大学里常见的数学指示,但是只要你开动脑筋,用你所学的七年级数学知识同样可以完美解决,敢不敢挑战一下?相信自己是最棒的!形如$|\begin{array}{l}{a}&{c}\\{b}&{d}\end{array}|$的式子叫做二阶行列式,它的运算法则用公式表示为$|\begin{array}{l}{a}&{c}\\{b}&{d}\end{array}|$=ad-bc,解决以下问题:(1)你能仿照上面的解释,表示$|\begin{array}{l}{m}&{p}\\{n}&{q}\end{array}|$出的结果吗?
(2)依此法则计算$|\begin{array}{l}{2}&{1}\\{-3}&{4}\end{array}|$的结果是多少?
(3)再进一步,挑战一下!如果$|\begin{array}{l}{5}&{3}\\{x+1}&{x}\end{array}|$=4,那么x的值为多少?
分析 (1)根据题中的新定义化简原式即可;
(2)原式利用题中的新定义计算即可得到结果;
(3)已知等式利用题中的新定义化简,计算即可求出x的值.
解答 解:(1)根据题意得:原式=mq-np;
(2)原式=8+3=11;
(3)已知等式化简得:5x-3(x+1)=4,
去括号得:5x-3x-3=4,
移项合并得:2x=7,
解得:x=3.5.
点评 此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
19.计算:(-12)+(+$\frac{6}{5}$)+(-8)+(-$\frac{7}{10}$)+(-$\frac{1}{2}$)=( )
| A. | -19 | B. | -18 | C. | -20 | D. | -17 |
20.已知点P在第四象限,且到x轴的距离为2,则点P的坐标为( )
| A. | (4,-2) | B. | (-4,2) | C. | (-2,4) | D. | (2,-4) |
17.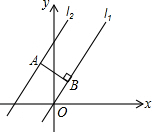 如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为$y=\frac{4}{3}x+4$,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )
如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为$y=\frac{4}{3}x+4$,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )
 如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为$y=\frac{4}{3}x+4$,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )
如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为$y=\frac{4}{3}x+4$,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | $\frac{12}{5}$ |
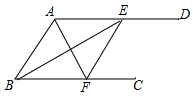 如图,AD∥BC,AF平分∠BAD交BC于点F,BE平分∠ABC交AD于点E.求证:
如图,AD∥BC,AF平分∠BAD交BC于点F,BE平分∠ABC交AD于点E.求证:
 如图,在△ABC中,已知AD是BC边上的高,DC=1,BD=2,tanB=cos∠DAC,则AB的值为$\sqrt{7}$.
如图,在△ABC中,已知AD是BC边上的高,DC=1,BD=2,tanB=cos∠DAC,则AB的值为$\sqrt{7}$.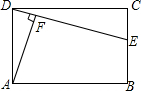 如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.
如图所示,在矩形ABCD中,E是BC上一点,AF⊥DE于点F.