题目内容
8．若两个相似三角形对应中线的比是2：3，它们的周长之和为15，则较小的三角形周长为6．分析 利用相似三角形的周长比等于相似比，根据它们的周长之和为15，即可得到结论．
解答 解：∵两个相似三角形的对应中线的比为2：3，
∴它们的周长比为2：3，
∵它们的周长之和为15，
∴较小的三角形周长为15×$\frac{2}{2+3}$=6．
故答案为：6．
点评 本题考查对相似三角形性质（1）相似三角形周长的比等于相似比；（2）相似三角形面积的比等于相似比的平方；（3）相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．
练习册系列答案
相关题目
19．计算：（-12）+（+$\frac{6}{5}$）+（-8）+（-$\frac{7}{10}$）+（-$\frac{1}{2}$）=（ ）
| A． | -19 | B． | -18 | C． | -20 | D． | -17 |
3．下表中的字母都是按移动规律排列的．
我们把某格中的字母的和所得多项式称为特征多项式，例如第1格的“特征多项式”为6x+2y，第2格的“特征多项式”为9x+4y，回答下列问题．
（1）第3格的“特征多项式”为12x+6y，第4格的“特征多项式”为15x+8y，第n格的“特征多项式”为3（n+1）x+2ny（n为正整数）；
（2）求第6格的“特征多项式”与第5格的“特征多项式”的差．
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x y x x | x x x y y x x x y y x x x | x x x x y y y x x x x y y y x x x x | … |
（1）第3格的“特征多项式”为12x+6y，第4格的“特征多项式”为15x+8y，第n格的“特征多项式”为3（n+1）x+2ny（n为正整数）；
（2）求第6格的“特征多项式”与第5格的“特征多项式”的差．
如图，路边一棵树AB，身高1.8m的小明站在水平地面BD的D处，从点C测得树的顶端A的仰角为60°．测得树的底部B的俯角为30°，求树高AB．
20．已知点P在第四象限，且到x轴的距离为2，则点P的坐标为（ ）
| A． | （4，-2） | B． | （-4，2） | C． | （-2，4） | D． | （2，-4） |
17．
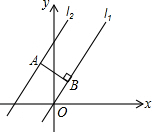如图，在平面直角坐标系中，已知l1∥l2，直线l1经过原点O，直线l2对应的函数表达式为$y=\frac{4}{3}x+4$，点A在直线l2上，AB⊥l1，垂足为B，则线段AB的长为（ ）
如图，在平面直角坐标系中，已知l1∥l2，直线l1经过原点O，直线l2对应的函数表达式为$y=\frac{4}{3}x+4$，点A在直线l2上，AB⊥l1，垂足为B，则线段AB的长为（ ）| A． | 2 | B． | 3 | C． | 4 | D． | $\frac{12}{5}$ |
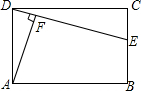如图所示，在矩形ABCD中，E是BC上一点，AF⊥DE于点F．