题目内容
12.某市出租车收费标准是:起步价10元,可乘3千米,3千米到5千米,每千米1.3元,超过5千米,每千米2.4元(1)若小李乘坐了x(x>5)千米的路程,则小李所支付的费用是多少(用代数式表示)?
(2)若小马乘坐的路程为15千米,则小马应付的费用是多少?
(3)若小张租一次车付了24.6元,求小张租车所走的路程.
分析 (1)根据题意可以知道前3千米支付10元,3千米到5千米支付1.3×(5-3)元,超过5千米支付的费用为2.4(x-5),从而可以求得问题的答案;
(2)把小马乘坐的路程数据代入(1)的代数式可求小马应付的费用是多少;
(3)可以判断出24.6元车费是否在这个范围内,用x>5的关系式计算即可求解.
解答 解:(1)小李所支付的费用是10+2.6+2.4(x-5)元;
(2)10+2.6+2.4×(15-5)
=10+2.6+24
=36.6(元)
答:小马应付的费用是36.6元;
(3)依题意有
10+2.6+2.4(x-5)=24.6,
解得x=10.
答:小张租车所走的路程是10千米.
点评 本题考查一元一次方程的应用,列代数式和代数式的求值,解题的关键是明确题意,根据题意列出符合要求的代数式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.下表中的字母都是按移动规律排列的.
我们把某格中的字母的和所得多项式称为特征多项式,例如第1格的“特征多项式”为6x+2y,第2格的“特征多项式”为9x+4y,回答下列问题.
(1)第3格的“特征多项式”为12x+6y,第4格的“特征多项式”为15x+8y,第n格的“特征多项式”为3(n+1)x+2ny(n为正整数);
(2)求第6格的“特征多项式”与第5格的“特征多项式”的差.
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x y x x | x x x y y x x x y y x x x | x x x x y y y x x x x y y y x x x x | … |
(1)第3格的“特征多项式”为12x+6y,第4格的“特征多项式”为15x+8y,第n格的“特征多项式”为3(n+1)x+2ny(n为正整数);
(2)求第6格的“特征多项式”与第5格的“特征多项式”的差.
20.已知点P在第四象限,且到x轴的距离为2,则点P的坐标为( )
| A. | (4,-2) | B. | (-4,2) | C. | (-2,4) | D. | (2,-4) |
17.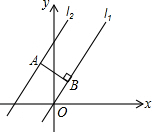 如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为$y=\frac{4}{3}x+4$,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )
如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为$y=\frac{4}{3}x+4$,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )
 如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为$y=\frac{4}{3}x+4$,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )
如图,在平面直角坐标系中,已知l1∥l2,直线l1经过原点O,直线l2对应的函数表达式为$y=\frac{4}{3}x+4$,点A在直线l2上,AB⊥l1,垂足为B,则线段AB的长为( )| A. | 2 | B. | 3 | C. | 4 | D. | $\frac{12}{5}$ |
2.下列每一组数据中的三个数值分别为三角形的三边长,能构成直角三角形的是( )
| A. | 3、4、5 | B. | 7、8、9 | C. | 1、2、3 | D. | 6、12、13 |
 如图,在边长为$2\sqrt{3}$的等边三角形ABC中,以点A为圆心的圆与边BC相切,与边AB、AC相交于点D、E,则图中阴影部分的面积为$3\sqrt{3}-\frac{3}{2}π$.
如图,在边长为$2\sqrt{3}$的等边三角形ABC中,以点A为圆心的圆与边BC相切,与边AB、AC相交于点D、E,则图中阴影部分的面积为$3\sqrt{3}-\frac{3}{2}π$.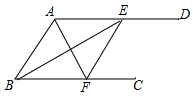 如图,AD∥BC,AF平分∠BAD交BC于点F,BE平分∠ABC交AD于点E.求证:
如图,AD∥BC,AF平分∠BAD交BC于点F,BE平分∠ABC交AD于点E.求证: 如图,在△ABC中,已知AD是BC边上的高,DC=1,BD=2,tanB=cos∠DAC,则AB的值为$\sqrt{7}$.
如图,在△ABC中,已知AD是BC边上的高,DC=1,BD=2,tanB=cos∠DAC,则AB的值为$\sqrt{7}$.