题目内容
17.化简:($\frac{x+1}{{x}^{2}-x}$-$\frac{x}{{x}^{2}-2x+1}$)÷$\frac{1}{x}$+$\frac{{x}^{2}}{(x-1)^{2}}$.分析 原式第一项括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分后合并即可得到结果.
解答 解:原式=[$\frac{x+1}{x(x-1)}$-$\frac{x}{(x-1)^{2}}$]•x+$\frac{{x}^{2}}{(x-1)^{2}}$=$\frac{{x}^{2}-1-{x}^{2}}{x(x-1)^{2}}$•x+$\frac{{x}^{2}}{(x-1)^{2}}$=-$\frac{1}{(x-1)^{2}}$+$\frac{{x}^{2}}{(x-1)^{2}}$=$\frac{(x+1)(x-1)}{(x-1)^{2}}$=$\frac{x+1}{x-1}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
7.某地为了缓解旱情进行了一场人工降雨,现测得6个面积相等区域的降雨量如下表所示:
则这6个区域降雨量的众数和平均数分别为( )
| 区域 | 1 | 2 | 3 | 4 | 5 | 6 |
| 降雨量(mm) | 14 | 12 | 13 | 13 | 17 | 15 |
| A. | 13,13.8 | B. | 14,15 | C. | 13,14 | D. | 14,14.5 |
5.下列代数式中是二次二项式的是( )
| A. | xy-1 | B. | $\frac{1}{{x}^{2}+1}$ | C. | x2+xy2 | D. | $\sqrt{{x}^{4}+1}$ |
2. 如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是( )
如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是( )
 如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是( )
如图,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E,连接EC,则∠AEC的度数是( )| A. | 115° | B. | 75° | C. | 105° | D. | 50° |
6.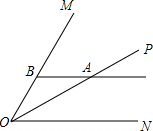 如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=4.则直线AB与ON之间的距离是( )
如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=4.则直线AB与ON之间的距离是( )
 如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=4.则直线AB与ON之间的距离是( )
如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=4.则直线AB与ON之间的距离是( )| A. | $\sqrt{3}$ | B. | 2 | C. | $2\sqrt{3}$ | D. | 4 |
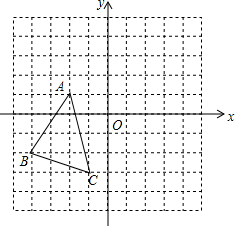 如图,在平面直角坐标系中,△ABC的顶点都在网格点上,将△ABC先向右平移5个单位长度,再向上平移2个单位长度,得到△A′B′C′.
如图,在平面直角坐标系中,△ABC的顶点都在网格点上,将△ABC先向右平移5个单位长度,再向上平移2个单位长度,得到△A′B′C′. 如图,菱形ABCD的边长为5cm,对角线BD的长为6cm,则菱形ABCD的面积为24cm2.
如图,菱形ABCD的边长为5cm,对角线BD的长为6cm,则菱形ABCD的面积为24cm2.