题目内容
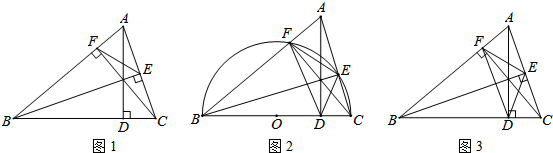
9. 如图,菱形ABCD的边长为5cm,对角线BD的长为6cm,则菱形ABCD的面积为24cm2.
如图,菱形ABCD的边长为5cm,对角线BD的长为6cm,则菱形ABCD的面积为24cm2.
分析 由菱形ABCD的边长为5cm,对角线BD的长为6cm,利用勾股定理即可求得OA的长,继而求得对角线AC的长,然后由菱形的面积等于对角线积的一半,求得答案.
解答 解:∵四边形ABCD是菱形,
∴AC⊥BD,OB=$\frac{1}{2}$BD=$\frac{1}{2}$×6=3(cm),
∴OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4(cm),
∴AC=2OA=8cm,
∴S菱形ABCD=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×6×8=24(cm2).
故答案为:24.
点评 此题考查了菱形的性质以及勾股定理.注意掌握菱形的面积等于对角线积的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )
 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )| A. | 圆柱 | B. | 球 | C. | 圆锥 | D. | 棱柱 |
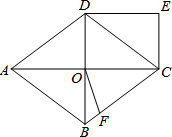 如图,菱形ABCD中,对角线AC,BD交于O点,DE∥AC,CE∥BD.
如图,菱形ABCD中,对角线AC,BD交于O点,DE∥AC,CE∥BD.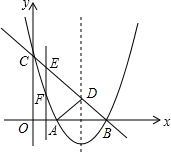 如图,某抛物线顶点坐标为(2,-1)与y轴交于点C(0,3),与x轴交于A、B两点
如图,某抛物线顶点坐标为(2,-1)与y轴交于点C(0,3),与x轴交于A、B两点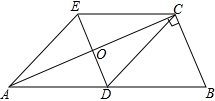 如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.