题目内容
8.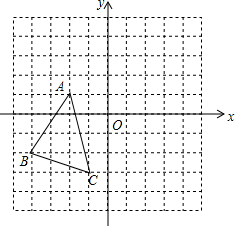 如图,在平面直角坐标系中,△ABC的顶点都在网格点上,将△ABC先向右平移5个单位长度,再向上平移2个单位长度,得到△A′B′C′.
如图,在平面直角坐标系中,△ABC的顶点都在网格点上,将△ABC先向右平移5个单位长度,再向上平移2个单位长度,得到△A′B′C′.(1)作出△A′B′C′;
(2)△A'B'C'的三个顶点坐标分别是
A′(3,3)、B′(1,0)、C′(4,-1);
(3)求△ABC的面积.
分析 (1)分别作出点A、B、C向右平移5个单位长度,再向上平移2个单位长度的点,然后顺次连接;
(2)根据网格结构写出各点的坐标;
(3)用三角形所在四边形的面积减去三个小三角形的面积即可求解.
解答 解:(1)所作图形如图所示:
(2)A'( 3,3)、B'( 1,0 )、C'(4,-1);
(3)S△ABC=4×3-1×4×$\frac{1}{2}$-2×3×$\frac{1}{2}$-1×3×$\frac{1}{2}$
=5.5.
故答案为:3,3,1,0,4,-1.
点评 本题考查了根据平移变换作图,解答本题的关键是根据网格结构作出对应点的位置,然后顺次连接.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
18.把a$\sqrt{-\frac{1}{a}}$根号外的因式移到根号内,化简的结果是( )
| A. | $\sqrt{a}$ | B. | $\sqrt{-a}$ | C. | -$\sqrt{a}$ | D. | -$\sqrt{-a}$ |
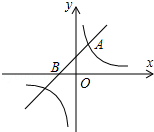 如图,一次函数y=x+1的图象与反比例函数$y=\frac{k}{x}$(k为常数,且k≠0)的图象都经过点A(m,2).
如图,一次函数y=x+1的图象与反比例函数$y=\frac{k}{x}$(k为常数,且k≠0)的图象都经过点A(m,2).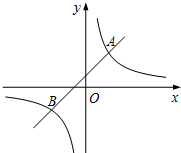 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.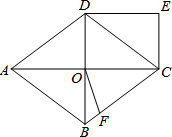 如图,菱形ABCD中,对角线AC,BD交于O点,DE∥AC,CE∥BD.
如图,菱形ABCD中,对角线AC,BD交于O点,DE∥AC,CE∥BD.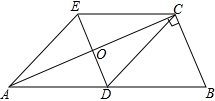 如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.