题目内容
15. 如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AE∥DF,AE=DF,CE=BF.求证:AB∥CD.
如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AE∥DF,AE=DF,CE=BF.求证:AB∥CD.
分析 由平行线的性质得出∠AEB=∠DFC,证出CF=BE,由SAS证明∠B=∠C,即可得出结论.
解答 证明:∵AE∥DF,
∴∠AEB=∠DFC,
∵CE=BF,
∴CF=BE,
在△ABE和△DCF中,$\left\{\begin{array}{l}{AE=DF}&{\;}\\{∠AEB=∠DFC}&{\;}\\{BE=CF}&{\;}\end{array}\right.$,
∴△ABE≌△DCF(SAS),
∴∠B=∠C,
∴AB∥CD.
点评 本题考查了平行线的性质与判定,全等三角形的性质和判定的应用;证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
5.关于概率,下列说法正确的是( )
| A. | 莒县“明天降雨的概率是75%”表明明天莒县会有75%的时间会下雨 | |
| B. | 随机抛掷一枚质地均匀的硬币,落地后一定反面向上 | |
| C. | 在一次抽奖活动中,中奖的概率是1%,则抽奖100次就一定会中奖 | |
| D. | 同时抛掷两枚质地均匀硬币,“一枚硬币正面向上,一枚硬币反面向上”的概率是$\frac{1}{2}$ |
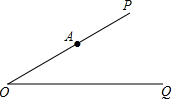 如图,∠POQ=30°,点A在OP边上,且OA=6,试在OQ边上确定一点B,使得△AOB是等腰三角形,则满足条件的点B个数为( )
如图,∠POQ=30°,点A在OP边上,且OA=6,试在OQ边上确定一点B,使得△AOB是等腰三角形,则满足条件的点B个数为( ) 如图,试写出x的取值范围,并根据x的取值范围化简:$\sqrt{{x}^{2}+2x+1}$-|2-x|.
如图,试写出x的取值范围,并根据x的取值范围化简:$\sqrt{{x}^{2}+2x+1}$-|2-x|.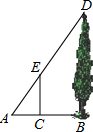 如图,某学生想利用标杆测量一棵大树的高度,如果标杆EC的高为1.8m,并测得AC=0.9m,AB=2.1m,那么大树DB的高度是4.2m.
如图,某学生想利用标杆测量一棵大树的高度,如果标杆EC的高为1.8m,并测得AC=0.9m,AB=2.1m,那么大树DB的高度是4.2m.