题目内容
4．
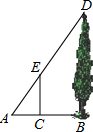如图，某学生想利用标杆测量一棵大树的高度，如果标杆EC的高为1.8m，并测得AC=0.9m，AB=2.1m，那么大树DB的高度是4.2m．
分析 先根据相似三角形的判定定理得出Rt△ACE∽Rt△ABD，再根据相似三角形的对应边成比例即可求出BD的长．
解答 解：∵EC∥AB，BD⊥AB，
∴EC∥BD，∠ACE=∠ABD=90°，
在Rt△ACE∽Rt△ABD中，∠A=∠A，∠ACE=∠ABD=90°，
∴Rt△ACE∽Rt△ABD，
∴$\frac{AC}{AB}$=$\frac{EC}{DB}$，即$\frac{0.9}{2.1}$=$\frac{1.8}{DB}$，解得DB=4.2m．
故答案为：4.2．
点评 本题考查的是相似三角形的应用，用到的知识点为：相似三角形的对应边成比例．
练习册系列答案
备战中考寒假系列答案
相关题目
如图，这个图形是一个轴对称图形，它有8条对称轴．
如图，点C、E、F、B在同一直线上，点A、D在BC异侧，AE∥DF，AE=DF，CE=BF．求证：AB∥CD．
如图，B、E、F、C四点在同一条直线上，∠A=∠D，BE=CF，∠B=∠C．求证：OA=OD．
已知：抛物线y=ax2-2（a-1）x+a-2（a＞0）．
9．抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如表：
从表可知，
①抛物线与x轴的交点为（-2，0）和（3，0）；
②抛物线的对称轴是x=$\frac{1}{2}$；
③函数y=ax2+bx+c的最大值为$\frac{25}{4}$；
④x＜$\frac{1}{2}$，y随x增大而增大．
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与x轴的交点为（-2，0）和（3，0）；
②抛物线的对称轴是x=$\frac{1}{2}$；
③函数y=ax2+bx+c的最大值为$\frac{25}{4}$；
④x＜$\frac{1}{2}$，y随x增大而增大．
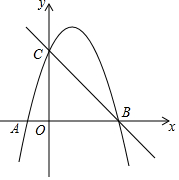如图，在平面直角坐标系中，O为坐标原点，抛物线y=ax2-2ax+3与x轴交于A、B两点，与y轴交于点C，过B、C两点的直线解析式为y=-x+b．
在平面直角坐标系xOy中，己知A（-1，5），B（4，2），C（-1，0）三点．