题目内容
7．
如图，试写出x的取值范围，并根据x的取值范围化简：$\sqrt{{x}^{2}+2x+1}$-|2-x|．
分析 根据数轴确定x的取值范围，根据二次根式的性质化简即可．
解答 解：x的取值范围是-1＜x≤2，
∴x+1＞0，2-x≥0，
则$\sqrt{{x}^{2}+2x+1}$-|2-x|=|x+1|-|2-x|=x+1-2+x=2x-1．
点评 本题考查的是二次根式的化简，掌握二次根式的性质、绝对值的性质是解题的关键．
练习册系列答案
相关题目
17．一种零件的直径尺寸在图纸上是30${\;}_{-0.02}^{+0.03}$（单位：mm），它表示这种零件的标准尺寸是30mm，则加工要求尺寸最大不超过（ ）
| A． | 0.03mm | B． | 0.02mm | C． | 30.03mm | D． | 29.92mm |
18．已知m，n是方程x2-2x-2016=0的两个实数根，则n2+2m的值为于（ ）
| A． | 1010 | B． | 2012 | C． | 2016 | D． | 2020 |
如图，点C、E、F、B在同一直线上，点A、D在BC异侧，AE∥DF，AE=DF，CE=BF．求证：AB∥CD．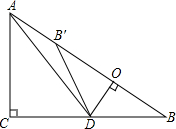
如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，点D为边CB上的一个动点（点D不与点B重合），过D作DO⊥AB，垂足为O，点B′在边AB上，且与点B关于直线DO对称，连接DB′，AD．
如图，B、E、F、C四点在同一条直线上，∠A=∠D，BE=CF，∠B=∠C．求证：OA=OD．
已知：抛物线y=ax2-2（a-1）x+a-2（a＞0）．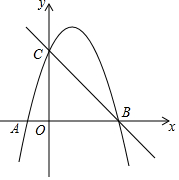
如图，在平面直角坐标系中，O为坐标原点，抛物线y=ax2-2ax+3与x轴交于A、B两点，与y轴交于点C，过B、C两点的直线解析式为y=-x+b．