题目内容
5.有六张正面分别标有数字-3,-2,0,1,2,3的不透明卡片,它们除数字不同外其他全部相同,现将它们背面朝上,洗匀后从中任取两张,将卡片上的数字分别做为点P的横、纵坐标,则P点落在抛物线y=x2+2x-3上的概率为$\frac{2}{15}$.分析 根据二次函数图象上点的坐标特征判断出在y=x2+2x-3上的情况数以及总情况数,然后根据概率公式列式计算即可得解.
解答 解:一共有30种等可能的情况,点P(x,y)落在二次函数y=x2+2x-3上图象的有 4种情况.
∴所求概率P=$\frac{4}{30}$=$\frac{2}{15}$.
故答案为$\frac{2}{15}$.
点评 本题考查了二次函数图象上点的坐标特征,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AE∥DF,AE=DF,CE=BF.求证:AB∥CD.
如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AE∥DF,AE=DF,CE=BF.求证:AB∥CD.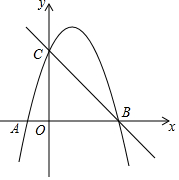 如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax+3与x轴交于A、B两点,与y轴交于点C,过B、C两点的直线解析式为y=-x+b.
如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2-2ax+3与x轴交于A、B两点,与y轴交于点C,过B、C两点的直线解析式为y=-x+b. 有理数a、b、c在数轴上的对应点如图所示,化简代数式|2a-b|+3|a+b|-|4c-a|=-4a-2b-4c.
有理数a、b、c在数轴上的对应点如图所示,化简代数式|2a-b|+3|a+b|-|4c-a|=-4a-2b-4c. 在平面直角坐标系xOy中,己知A(-1,5),B(4,2),C(-1,0)三点.
在平面直角坐标系xOy中,己知A(-1,5),B(4,2),C(-1,0)三点. 如图,已知l1∥l2∥l3,若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则EF=9.
如图,已知l1∥l2∥l3,若$\frac{AB}{BC}$=$\frac{2}{3}$,DE=6,则EF=9.