题目内容
8.计算:$\frac{cos30°-sin45°}{sin30°+cos45°}$.分析 把特殊角的三角函数值代入,根据二次根式的运算法则计算即可.
解答 解:原式=$\frac{\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}}{\frac{1}{2}+\frac{\sqrt{2}}{2}}$=$\sqrt{6}$-$\sqrt{3}$-2+$\sqrt{2}$.
点评 本题考查的是特殊角的三角函数值和二次根式的计算,解决此类题目的关键是熟记特殊角的三角函数值.

练习册系列答案
相关题目
18. 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0.其中正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0.其中正确的是( )
 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0.其中正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0.其中正确的是( )| A. | ①③ | B. | ② | C. | ②④ | D. | ③④ |
16.如果四个线段3,x,5,y的长度满足$\frac{3}{x}=\frac{5}{y}$,那么下列各式中不成立的一定是( )
| A. | $\frac{x}{y}=\frac{3}{5}$ | B. | $\frac{3+x}{x}=\frac{5+y}{y}$ | C. | $\frac{x}{y}=\frac{5}{3}$ | D. | $\frac{x-3}{3}=\frac{y-5}{5}$ |
13. 如图,△ABC中,∠C=60°,若沿图中虚线截去∠C,则∠1+∠2等于( )
如图,△ABC中,∠C=60°,若沿图中虚线截去∠C,则∠1+∠2等于( )
 如图,△ABC中,∠C=60°,若沿图中虚线截去∠C,则∠1+∠2等于( )
如图,△ABC中,∠C=60°,若沿图中虚线截去∠C,则∠1+∠2等于( )| A. | 360° | B. | 240° | C. | 180° | D. | 140° |
17.下列各式中计算正确的是( )
| A. | (2x-y)2=4x2+y2-2xy | B. | (a2+2b)2=a2+4a2b+4b2 | ||
| C. | (a-b)2=a2-b2 | D. | ($\frac{1}{2}$x+3)2=$\frac{1}{4}$x2+3x+9 |
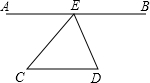 如图,已知点A,E,B在一同条直线上,设∠CED=x,∠C+∠D=y.
如图,已知点A,E,B在一同条直线上,设∠CED=x,∠C+∠D=y.