题目内容
13．
如图，△ABC中，∠C=60°，若沿图中虚线截去∠C，则∠1+∠2等于（ ）| A． | 360° | B． | 240° | C． | 180° | D． | 140° |
分析 先利用三角形内角与外角的关系，得出∠1+∠2=∠C+（∠C+∠3+∠4），再根据三角形内角和定理即可得出结果．
解答 解：如图，
∵∠1、∠2是△CDE的外角，
∴∠1=∠4+∠C，∠2=∠3+∠C，
即∠1+∠2=∠C+（∠C+∠3+∠4）=60°+180°=240°，
故选：B．
点评 此题主要考查了三角形内角和定理及外角的性质，三角形内角和是180°；三角形的任一外角等于和它不相邻的两个内角之和．
练习册系列答案
相关题目
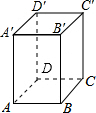如图，正四棱柱的底面边长为4cm，侧棱长为8cm，一只蚂蚁从正四棱柱底面上的顶点A沿棱柱的表面到顶点C′处吃食物，那么蚂蚁走最短路线的路径为8$\sqrt{2}$cm．
4．
实数a在数轴上的位置如图，则下列关系表示正确的是 （ ）
实数a在数轴上的位置如图，则下列关系表示正确的是 （ ）| A． | a＜1＜-a | B． | a＜-a＜1 | C． | 1＜-a＜a | D． | -a＜a＜1 |
3．
如图，△ABC中，∠ABC=∠ACB，∠A=50°，P是△ABC内一点，且∠1=∠2，则∠BPC等于（ ）
如图，△ABC中，∠ABC=∠ACB，∠A=50°，P是△ABC内一点，且∠1=∠2，则∠BPC等于（ ）| A． | 115° | B． | 125° | C． | 130° | D． | 140° |