题目内容
19.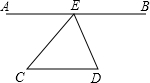 如图,已知点A,E,B在一同条直线上,设∠CED=x,∠C+∠D=y.
如图,已知点A,E,B在一同条直线上,设∠CED=x,∠C+∠D=y.(1)若AB∥CD,试求含x的式子表示y,并写出x的取值范围;
(2)若x=90°,且∠AEC与∠D互余,求证:AB∥CD.
分析 (1)由平行线的性质可得到∠AEC=∠C,∠BED=∠D,在△CDE中利用三角形内角和定理可得到y与x之间的关系式;
(2)由条件可证得∠BED=∠D,根据平行线的判定可证明AB∥CD.
解答 (1)解:
∵AB∥CD,
∴∠AEC=∠C,∠BED=∠D,
∵∠C+∠D=y,
∴∠AEC+∠BED=y,
∵∠CED=x,∠AEC+∠CED+∠BED=180°,
∴x+y=180°,
∴y=180°-x,其中x的取值范围是0°<x<180°;
(2)证明:
∵x=90°,即∠CED=90°,
∴∠AEC+∠BED=90°,
∵∠AEC与∠D互余,
∴∠AEC+∠D=90°,
∴∠BED=∠D,
∴AB∥CD.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
4. 实数a在数轴上的位置如图,则下列关系表示正确的是 ( )
实数a在数轴上的位置如图,则下列关系表示正确的是 ( )
 实数a在数轴上的位置如图,则下列关系表示正确的是 ( )
实数a在数轴上的位置如图,则下列关系表示正确的是 ( )| A. | a<1<-a | B. | a<-a<1 | C. | 1<-a<a | D. | -a<a<1 |
9.-xn与(-x)n的正确关系是( )
| A. | 相等 | |
| B. | 互为相反数 | |
| C. | 当n为奇数时它们互为相反数,当n为偶数时相等 | |
| D. | 当n为奇数时相等,当n为偶数时互为相反数 |
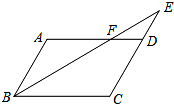 如图,在平行四边形ABCD中,点E是CD延长线上一点,BE与AD交于点F,若CD=2DE,且△DEF的面积为3,则三角形ABF的面积为( )
如图,在平行四边形ABCD中,点E是CD延长线上一点,BE与AD交于点F,若CD=2DE,且△DEF的面积为3,则三角形ABF的面积为( )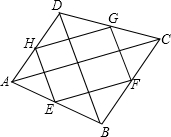 我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形,如图,E、F、G、H分别是四边形ABCD各边的中点,可证中点四边形EFGH是平行四边形,如果我们对四边形ABCD的对角线AC与BD添加一定的条件,则可使中点四边形EFGH成为特殊的平行四边形,请你经过探究后回答下面问题?
我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形,如图,E、F、G、H分别是四边形ABCD各边的中点,可证中点四边形EFGH是平行四边形,如果我们对四边形ABCD的对角线AC与BD添加一定的条件,则可使中点四边形EFGH成为特殊的平行四边形,请你经过探究后回答下面问题?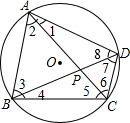 如图,圆内接四边形ABCD的对角线AC、BD把它的4个内角分成8个角,AC、BD相交于点P.
如图,圆内接四边形ABCD的对角线AC、BD把它的4个内角分成8个角,AC、BD相交于点P.