题目内容
12.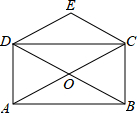 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( )
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
分析 由CE∥BD,DE∥AC,可证得四边形CODE是平行四边形,又由四边形ABCD是矩形,根据矩形的性质,易得OC=OD=2,即可判定四边形CODE是菱形,则可求得答案.
解答 解:
∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴AC=BD=4,OA=OC,OB=OD,
∴OD=OC=$\frac{1}{2}$AC=2,
∴四边形CODE是菱形,
∴四边形CODE的周长为:4OC=4×2=8.
故选C.
点评 本题主要考查了菱形的判定与性质以及矩形的性质.此题难度不大,注意证得四边形CODE是菱形是解此题的关键.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
3.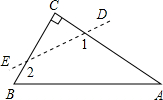 如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
 如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )| A. | 90° | B. | 135° | C. | 150° | D. | 270° |
20.把多项式3x2+y3-5xy2-x3,按x的升幂排列正确的是( )
| A. | y3-5xy2+3x2-x3 | B. | -x3+3x2-5xy2+y3 | C. | y3+5xy2+3x2+x3 | D. | 5xy2+3x2-x3+y3 |
4.关于x的方程x2+kx-1=0的根的情况描述正确的是( )
| A. | k为任何实数,方程都没有实数根 | |
| B. | k为任何实数,方程都有两个不相等的实数根 | |
| C. | k为任何实数,方程都有两个相等的实数根 | |
| D. | 根据 k 的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 |
1.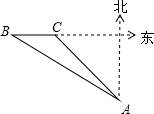 如图,海关缉私艇在A处接到情报,在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行,于是该艇立即沿北偏西45°的方向前进,经过1小时航行,恰好在C处截住可疑船只,则缉私艇的速度为( )
如图,海关缉私艇在A处接到情报,在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行,于是该艇立即沿北偏西45°的方向前进,经过1小时航行,恰好在C处截住可疑船只,则缉私艇的速度为( )
 如图,海关缉私艇在A处接到情报,在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行,于是该艇立即沿北偏西45°的方向前进,经过1小时航行,恰好在C处截住可疑船只,则缉私艇的速度为( )
如图,海关缉私艇在A处接到情报,在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行,于是该艇立即沿北偏西45°的方向前进,经过1小时航行,恰好在C处截住可疑船只,则缉私艇的速度为( )| A. | (12$\sqrt{2}$+12$\sqrt{6}$)海里/时 | B. | (12$\sqrt{3}$+12$\sqrt{6}$)海里/时 | C. | (12$\sqrt{2}$+12$\sqrt{3}$)海里/时 | D. | (8$\sqrt{3}$+8$\sqrt{6}$)海里/时 |
2. 如图为一根圆柱形的空心钢管,它的主视图是( )
如图为一根圆柱形的空心钢管,它的主视图是( )
 如图为一根圆柱形的空心钢管,它的主视图是( )
如图为一根圆柱形的空心钢管,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
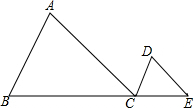 如图,在△ABC中,AC=9,AB=6,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=3,点E是线段BC延长线上的动点,当△ABC和△DCE相似时,线段CE的长为2或4.5.
如图,在△ABC中,AC=9,AB=6,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=3,点E是线段BC延长线上的动点,当△ABC和△DCE相似时,线段CE的长为2或4.5.