题目内容
17.观察下面三行数:-3,9,-27,81,-243,…
-5,7,-29,79,-245,…
-1,3,-9,27,-81,…
(1)探索第一行数中的规律,并用含n的代数式表示第n个数:(-3)n;
(2)第二、三行数与第一行数中相对应的数分别有什么关系?
(3)分别取上边三行数中的第6个数,计算取出的三个数的和.
分析 (1)第1行的各数是-3的序数次方,据此可得;
(2)第二行数是第一行相应的数减2、第三行数是第一行相应的数除以3;
(3)由以上所得规律,将第7个数相加即可得.
解答 解:(1)第一行数的规律是:-3,(-3)2,(-3)3,(-3)4,(-3)5,….
因此第n 个数是:(-3)n,
故答案为:(-3)n;
(2)对比第一、二两行数中位置对应的数,可以发现:第二行数是第一行相应的数减2,
即:-3-2,(-3)2-2,(-3)3-2,(-3)4-2,(-3)5-2,….
对比第一、第三两行中位置对应的数,可以发现:第三行数是第一行相应的数除以3,
即-3÷3,(-3)2÷3,(-3)3÷3,(-3)4÷3,(-3)5÷3;
(3)每行中的第6个数的和是:
(-3)6+[(-3)6-2]+[(-3)6÷3]
=729+727+243
=1699.
点评 本题主要考查数字的变化类,由数字的变化得出第1行各数是-3的序数次方及第2、3行各数与第1行各数的关系是解题的关键.

练习册系列答案
相关题目
8.$\frac{1}{2}$-$\frac{1}{6}$-$\frac{1}{12}$-$\frac{1}{20}$-$\frac{1}{30}$=( )
| A. | $\frac{1}{6}$ | B. | -$\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{6}$ |
2.小壮同学的体重为56.4千克,这个数是四舍五入得来的,那么你认为小壮的体重M千克的范围是( )
| A. | 56.35≤M<56.45 | B. | 56.39<M≤56.44 | C. | 56.41<M<56.50 | D. | 56.44<M<56.59 |
9.已知一个样本1,3,2,x,4的平均数是3,则这个样本的方差是( )
| A. | 2 | B. | 2.5 | C. | 10 | D. | $\frac{6}{5}$ |
6.关于x的一元二次方程x2+(m-2)x-2m=0有两个相等的实数根,则m的值是( )
| A. | -2 | B. | 2 | C. | 4+±$\sqrt{2}$ | D. | 0或8 |
7.下列各式中是二次根式的是( )
| A. | $\root{4}{8}$ | B. | $\sqrt{-7}$ | C. | $\sqrt{{a}^{2}+3}$ | D. | $\root{3}{9}$ |
 如图,∠BOC在∠AOB的外部,∠AOC与∠BOC互为补角,OD平分∠AOC,∠BOD:∠BOC=3:4,求∠BOD的度数.
如图,∠BOC在∠AOB的外部,∠AOC与∠BOC互为补角,OD平分∠AOC,∠BOD:∠BOC=3:4,求∠BOD的度数.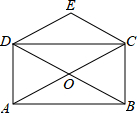 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( )
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( )