题目内容
1.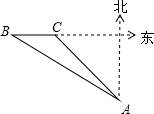 如图,海关缉私艇在A处接到情报,在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行,于是该艇立即沿北偏西45°的方向前进,经过1小时航行,恰好在C处截住可疑船只,则缉私艇的速度为( )
如图,海关缉私艇在A处接到情报,在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行,于是该艇立即沿北偏西45°的方向前进,经过1小时航行,恰好在C处截住可疑船只,则缉私艇的速度为( )| A. | (12$\sqrt{2}$+12$\sqrt{6}$)海里/时 | B. | (12$\sqrt{3}$+12$\sqrt{6}$)海里/时 | C. | (12$\sqrt{2}$+12$\sqrt{3}$)海里/时 | D. | (8$\sqrt{3}$+8$\sqrt{6}$)海里/时 |
分析 设AD=x海里,根据正切的概念用x表示出BD、CD,根据题意列出方程,解方程求出x,求出AC的长,得到答案.
解答 解: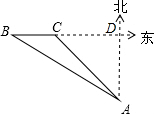 由题意得,BC=24海里,
由题意得,BC=24海里,
设AD=x海里,
在Rt△ABD中,BD=$\frac{AD}{tan∠B}$=$\sqrt{3}$x,
在Rt△ACD中,∠ACD=45°,
∴CD=AD=x,
则$\sqrt{3}$x-x=24,
解得,x=12$\sqrt{3}$+12,
∴AC=$\sqrt{2}$x=12$\sqrt{2}$+12$\sqrt{6}$,
∴缉私艇的速度为(12$\sqrt{2}$+12$\sqrt{6}$)海里/时,
故选:A.
点评 本题考查的是解直角三角形的应用,掌握锐角三角函数的概念、正确标注方向角是解题的关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
9.已知一个样本1,3,2,x,4的平均数是3,则这个样本的方差是( )
| A. | 2 | B. | 2.5 | C. | 10 | D. | $\frac{6}{5}$ |
16.下列实数最小的是( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$-1 | D. | 2-$\sqrt{2}$ |
6.关于x的一元二次方程x2+(m-2)x-2m=0有两个相等的实数根,则m的值是( )
| A. | -2 | B. | 2 | C. | 4+±$\sqrt{2}$ | D. | 0或8 |
13.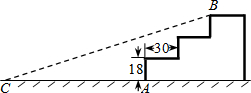 如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
 如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )| A. | 270cm | B. | 210cm | C. | 180cm | D. | 96cm |
11.若代数式-$\sqrt{x+3}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥-3 | B. | x>3 | C. | x≥3 | D. | x≤3 |
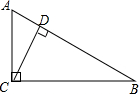 如图,∠ACB=90°,CD⊥AB,垂足为D,AB=13cm,AC=5cm,BC=12cm,那么点B到AC的距离是12cm,点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.
如图,∠ACB=90°,CD⊥AB,垂足为D,AB=13cm,AC=5cm,BC=12cm,那么点B到AC的距离是12cm,点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.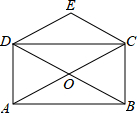 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( )
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( ) 如图,直角边长为$\sqrt{2}$的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )
如图,直角边长为$\sqrt{2}$的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )


