题目内容
 如图,已知AB为⊙O的直径,C为⊙O上一点,CD与AB的延长线交于点D.
如图,已知AB为⊙O的直径,C为⊙O上一点,CD与AB的延长线交于点D.(1)若∠CAB=∠BCD,求证:CD是⊙O的切线;
(2)在(1)的条件下,若AB=BD,CD=6,sin∠BCD=
| 1 |
| 3 |
考点:切线的判定与性质,解直角三角形
专题:证明题
分析:(1)连接OC.欲证CD是⊙O的切线,只需证明OC⊥CD即可;
(2)由已知条件“OB=OA=OC=
AB,AB=BD”证得OD=3OC;然后根据(1)中切线的性质在直角三角形OCD中利用勾股定理求得OC的长度;最后利用等量代换、三角函数的定义知sin∠BCD=sin∠CAB=
=
,从而求得CB的长度.
(2)由已知条件“OB=OA=OC=
| 1 |
| 2 |
| CB |
| AB |
| 1 |
| 3 |
解答: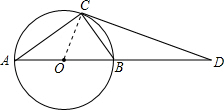 (1)证明:连接OC.
(1)证明:连接OC.
∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角);
又∵OA=OC(⊙O的半径),
∴∠CAO=∠OCA,即∠CAB=∠OCA(等边对等角);
∵∠CAB=∠BCD(已知),
∴∠BCD=∠OCA,
∴∠OCA+∠OCB=∠BCD+∠OCB,即∠ACB=∠OCD=90°,
∴OC⊥CD,
即CD是⊙O的切线;
(2)解:∵OB=OA=OC=
AB,AB=BD,
∴OD=3OC;
由(1)知,∠OCD=90°.则在Rt△OCD中,OD2=OC2+CD2,CD=6,
∴OC=
∴AB=2OC=3
;
∵∠OCA+∠OCB=∠BCD+∠OCB=90°,∠CAB=∠OCA,
∴∠BCD=∠CAB,
∴sin∠BCD=sin∠CAB=
=
,
∴CB=
AB=
,
即CB=
.
 (1)证明:连接OC.
(1)证明:连接OC.∵AB是⊙O的直径,
∴∠ACB=90°(直径所对的圆周角是直角);
又∵OA=OC(⊙O的半径),
∴∠CAO=∠OCA,即∠CAB=∠OCA(等边对等角);
∵∠CAB=∠BCD(已知),
∴∠BCD=∠OCA,
∴∠OCA+∠OCB=∠BCD+∠OCB,即∠ACB=∠OCD=90°,
∴OC⊥CD,
即CD是⊙O的切线;
(2)解:∵OB=OA=OC=
| 1 |
| 2 |
∴OD=3OC;
由(1)知,∠OCD=90°.则在Rt△OCD中,OD2=OC2+CD2,CD=6,
∴OC=
3
| ||
| 2 |
∴AB=2OC=3
| 2 |
∵∠OCA+∠OCB=∠BCD+∠OCB=90°,∠CAB=∠OCA,
∴∠BCD=∠CAB,
∴sin∠BCD=sin∠CAB=
| CB |
| AB |
| 1 |
| 3 |
∴CB=
| 1 |
| 3 |
| 2 |
即CB=
| 2 |
点评:本题考查了切线的判定与性质、勾股定理以及解直角三角形.证明过半径的外端点且垂直于这条半径的直线是圆的切线是常用的方法,求圆的半径常常用勾股定理,这些方法十分重要,要熟练掌握.

练习册系列答案
相关题目
要使
、
、(2x-4)0三个式子都有意义,则x的取值范围应为( )
| x+1 |
| 1 | ||
|
A、x>
| ||
| B、x≥-1且x≠2 | ||
C、x>
| ||
D、
|
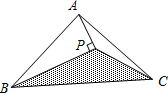 如图,△ABC的面积为1cm2,AP垂直∠B的平分线BP于P,则△PBC的面积为( )
如图,△ABC的面积为1cm2,AP垂直∠B的平分线BP于P,则△PBC的面积为( )| A、0.4 cm2 |
| B、0.5 cm2 |
| C、0.6 cm2 |
| D、0.7 cm2 |
对于素数p,q,方程x4-px3+q=0有整数解,则p=( )
| A、1 | B、2 | C、3 | D、4 |
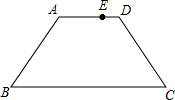 如图在梯形ABCD中AB=CD=5,AD=7,BC=13,E点在AD上,且AE=4,动点P从D出发沿着梯形的周界依次经过C、B最后到达A,设此过程中P点走过的距离为x,△APE的面积为y,把y表示成x的函数,并且画出图象.
如图在梯形ABCD中AB=CD=5,AD=7,BC=13,E点在AD上,且AE=4,动点P从D出发沿着梯形的周界依次经过C、B最后到达A,设此过程中P点走过的距离为x,△APE的面积为y,把y表示成x的函数,并且画出图象. 如图,边长为5的菱形ABCD中,AE⊥BC于点E,AE=4.以AE为边向右作正方形AEFG.边GF与CD交于点H,求FH的长.
如图,边长为5的菱形ABCD中,AE⊥BC于点E,AE=4.以AE为边向右作正方形AEFG.边GF与CD交于点H,求FH的长.