题目内容
16.某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果收件超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件,如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价x元(x为整数),每个月的销售量为y元.(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式.
分析 (1)当售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件,y=260-x,50≤x≤80,当如果售价超过80元后,若再涨价,则每涨1元每月少卖3件,y=420-3x,80<x<140,
(2)由利润=(售价-成本)×销售量列出函数关系式,
解答 解:(1)当50≤x≤80时,y=210-(x-50),即y=260-x,
当80<x<140时,y=210-(80-50)-3(x-80),即y=420-3x.
则$\left\{\begin{array}{l}{y=260-x(50≤x≤80)}\\{y=420-3x(80<x<140)}\end{array}\right.$,
(2)由利润=(售价-成本)×销售量可以列出函数关系式
w=-x2+300x-10400(50≤x≤80)
w=-3x2+540x-16800(80<x<140).
点评 本题主要考查二次函数的应用,应用二次函数解决实际问题比较简单.

练习册系列答案
相关题目
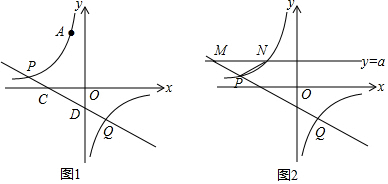
 如图,AB=DE,BC=EF,CD=FA,∠A=∠D,求证:∠ABC=∠DEF.
如图,AB=DE,BC=EF,CD=FA,∠A=∠D,求证:∠ABC=∠DEF. 如图,扇形OAB的圆心角为120°,半径为3cm,则该扇形的弧长为2πcm,面积为3πcm2.(结果保留π)
如图,扇形OAB的圆心角为120°,半径为3cm,则该扇形的弧长为2πcm,面积为3πcm2.(结果保留π)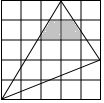 如图,在平面内5×5的正方形网格中,每个小正方形的边长为1,则图中阴影部分面积为$\frac{107}{60}$.
如图,在平面内5×5的正方形网格中,每个小正方形的边长为1,则图中阴影部分面积为$\frac{107}{60}$.