题目内容
11．已知，关于x的不等式组$\left\{\begin{array}{l}{x-a＞0}\\{2-x＞0}\end{array}\right.$的整数解共有两个，那么a的取值范围是-1≤a＜0．分析 首先解不等式组，利用a表示出不等式组的解集，然后根据不等式组有3个整数解，即可确定整数解，进而求得a的范围．
解答 解：$\left\{\begin{array}{l}{x-a＞0①}\\{2-x＞0②}\end{array}\right.$，
解①得x＞a，
解②得x＜2．
则不等式组的解集是a＜x＜2．
∵不等式组的整数解共有2个，
∴整数解是1，0．
则-1≤a＜0．
故答案是：-1≤a＜0．
点评 本题考查了不等式组的整数解，求不等式组的解集应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．下列说法正确的是（ ）
| A． | 4的平方根是-2 | B． | 8的立方根是±2 | ||
| C． | 任何实数都有平方根 | D． | 任何实数都有立方根 |
2．在直角坐标系中与（2，-3）在同一个正比例函数图象上的是（ ）
| A． | （2，3） | B． | （-2，-3） | C． | （4，-6） | D． | （-4，-6） |
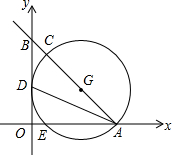如图，在直角坐标系中，直线AB与x、y轴分别交于点A（4，0）、B（0，$\frac{16}{3}$）两点，∠BAO的角平分线交y轴于点D，点C为直线AB上一点以AC为直径的⊙G经过点D，且与x轴交于另一点E．