题目内容
6.已知⊙O的半径为10cm.圆心O到直线l的距离OD=6cm.在直线l上有A、B、C三点,并且有AD=10cm,BD=8cm,CD=6cm,分别指出点A、B、C和⊙O的位置关系.分析 如图,连结OA、OB、OC,先分别利用勾股定理计算出OA、OB、OC的长,然后根据点与圆的位置关系的判定方法即可得到点A、B、C和⊙O的位置关系.
解答 解:如图,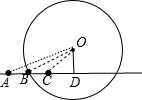 连结OA、OB、OC,
连结OA、OB、OC,
在Rt△OAD中,OA=$\sqrt{1{0}^{2}+{6}^{2}}$=2$\sqrt{34}$>10,
所以点A在⊙O外;
在Rt△OBD中,OB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
所以点B在⊙O上;
在Rt△OCD中,OC=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$<10,
所以点C在⊙O内.
点评 本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图,数轴上点A所对应的数是-$\sqrt{5}$.
如图,数轴上点A所对应的数是-$\sqrt{5}$.