题目内容
19. 如图,数轴上点A所对应的数是-$\sqrt{5}$.
如图,数轴上点A所对应的数是-$\sqrt{5}$.
分析 直角三角形中,利用勾股定理可以求出斜边的长度,即点A与原点的距离,可得出数轴上点A所表示的数.
解答 解:根据勾股定理可知该直角三角形斜边的长度为$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$,
∴点A到原点的距离是$\sqrt{5}$,
∵点A在原点的左侧,
∴点A表示的数是$-\sqrt{5}$,
故答案为:$-\sqrt{5}$.
点评 此题主要考查了勾股定理、实数与数轴之间的对应关系;熟练掌握勾股定理,并能进行推理计算是解决问题的关键,属中档题.

练习册系列答案
相关题目
14.如图所示是计算机某计算程序,若开始输入2,则最后输出的结果是( )


| A. | 6 | B. | 10 | C. | 22 | D. | 38 |
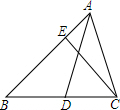 如图,已知:AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,则∠ADC的度数为70°.
如图,已知:AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,则∠ADC的度数为70°.