Question

14．求证：从正六边形的一个内角的顶点所引的三条对角线将这个角四等分．

Answer 1

分析 根据题意画出图形，写出已知、求证、再证明；由正六边形的性质得出各边相等，各个角为120°，由等腰三角形的性质得出∠BAC=∠FAE=30°，再由HL证明Rt△ACD≌Rt△AED，得出∠CAD=∠EAD=$\frac{1}{2}$∠CAE=30°，即可得出结论．

解答 已知：如图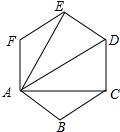，AC、AD、AE是正六边形的对角线；
求证：∠BAC=∠CAD=∠EAD=∠FAE；
证明：∵六边形ABCDEF是正六边形，
∴AB=BC=CD=DE=EF=FA，∠ABC=∠BCD=∠DEF=∠F=∠BAF=120°，
∴∠BAC=∠BCA=30°∠FAE=∠FEA=30°，
∴∠CAE=120°-30°-30°=60°，∠DCA=∠DEA=120°-30°=90°，
在Rt△ACD和Rt△AED中，$\left\{\begin{array}{l}{AD=AD}\\{CD=DE}\end{array}\right.$，
∴Rt△ACD≌Rt△AED（HL），
∴∠CAD=∠EAD=$\frac{1}{2}$∠CAE=30°，
∴∠BAC=∠CAD=∠EAD=∠FAE．

点评 本题考查了正六边形的性质、等腰三角形的性质、全等三角形的判定与性质；熟练掌握正六边形的性质是解决问题的关键．