题目内容
3.已知:二次函数的图象过点A(2,-3),且顶点坐标为C(1,-4).(1)求此二次函数的表达式;
(2)直接写出:当y≤0时,x的取值范围.
分析 (1)由于已知抛物线顶点坐标,则可设顶点式y=a(x-1)2-4,然后把A点坐标代入求出a即可;
(2)先根据抛物线与x轴的交点问题确定抛物线与x轴的交点坐标,然后写出抛物线不在x轴上方所对应的自变量的范围即可.
解答 解:(1)设抛物线解析式为y=a(x-1)2-4,
把A(2,-3)代入得a-4=-3,解得a=1,
所以抛物线解析式为y=(x-1)2-4;
(2)当y=0时,(x-1)2-4=0,解得x1=-1,x2=3,
所以抛物线与x轴的交点坐标为(-1,0),(3,0),
所以当-1≤x≤3时,y≤0.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列说法中正确的是( )
| A. | 想了解某种饮料中含色素的情况,宜采用抽样调查 | |
| B. | 某中学“学生艺术节”元旦汇演活动时下雨是必然事件 | |
| C. | 数据3,1,1,2,2的中位数是1 | |
| D. | 一组数据的波动越大,方差越小 |
8.△ABC的三条线高所在的直线相交于一点H,则点H在( )
| A. | △ABC内部 | B. | △ABC边上 | C. | △ABC的外部 | D. | 以上都有可能 |
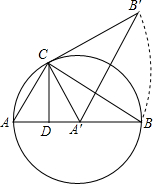 如图,点C是以AB为直径的圆周上一点,CD⊥AB于点D,已知AD=1,DB=3,现将三角形ABC绕顶点C逆时针旋转,当顶点A的对应点A′落在边AB的起始位置上即停止转动,则点B转过的路径长为$\frac{2\sqrt{3}}{3}$π.
如图,点C是以AB为直径的圆周上一点,CD⊥AB于点D,已知AD=1,DB=3,现将三角形ABC绕顶点C逆时针旋转,当顶点A的对应点A′落在边AB的起始位置上即停止转动,则点B转过的路径长为$\frac{2\sqrt{3}}{3}$π. 已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|,求a5+b5的值.
已知有理数a、b、c在数轴上的位置如图所示,且|a|=|b|,求a5+b5的值. 如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,求BC,BD的长度.
如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=8,求BC,BD的长度.