题目内容
在△ABC中，∠A，∠B，∠C所对的边分别为a，b，c，∠C=90°．若定义cotA=
=
，则称它为锐角A的余切，根据这个定义解答下列问题：
（1）cot30°= ；
（2）已知tanA=
，其中∠A为锐角，试求cotA的值；
（3）求证：tanA=cot（90°-∠A）．
| ∠A的邻边 |
| ∠A的对边 |
| b |
| a |
（1）cot30°=
（2）已知tanA=
| 3 |
| 4 |
（3）求证：tanA=cot（90°-∠A）．
考点：锐角三角函数的定义
专题：新定义
分析：（1）在Rt△ABC中，∠C=90°，设∠A=30°，根据直角三角形的性质用BC表示出AC的值，再根据余切的定义进行解答即可；
（2）在Rt△ABC中，∠C=90°，设BC=3k，则AC=4k，再根据余切的定义进行解答即可；
（3）在Rt△ABC中，∠C=90°，根据三角形内角和定理得出∠A+∠B=90°，∠B=90°-∠A，再根据三角函数的定义得出tanA=
，cotB=
，进而得到tanA=cot（90°-∠A）．
（2）在Rt△ABC中，∠C=90°，设BC=3k，则AC=4k，再根据余切的定义进行解答即可；
（3）在Rt△ABC中，∠C=90°，根据三角形内角和定理得出∠A+∠B=90°，∠B=90°-∠A，再根据三角函数的定义得出tanA=
| BC |
| AC |
| BC |
| AC |
解答：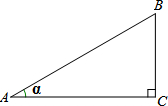
解：（1）如图，在Rt△ABC中，∠C=90°，
设∠A=30°，则AB=2BC，AC=
BC，
所以cot30°=
=
=
．
故答案为
；
（2）在Rt△ABC中，∠C=90°，
∵tanA=
=
，
∴可设BC=3k，则AC=4k，
∴cotA=
=
=
；
（3）在Rt△ABC中，∠C=90°，
则∠A+∠B=90°，
即∠B=90°-∠A，
∵tanA=
，cotB=
，
∴tanA=cotB，
即tanA=cot（90°-∠A）．
解：（1）如图，在Rt△ABC中，∠C=90°，设∠A=30°，则AB=2BC，AC=
| 3 |
所以cot30°=
| AC |
| BC |
| ||
| BC |
| 3 |
故答案为
| 3 |
（2）在Rt△ABC中，∠C=90°，
∵tanA=
| BC |
| AC |
| 3 |
| 4 |
∴可设BC=3k，则AC=4k，
∴cotA=
| AC |
| BC |
| 4k |
| 3k |
| 4 |
| 3 |
（3）在Rt△ABC中，∠C=90°，
则∠A+∠B=90°，
即∠B=90°-∠A，
∵tanA=
| BC |
| AC |
| BC |
| AC |
∴tanA=cotB，
即tanA=cot（90°-∠A）．
点评：本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．也考查了直角三角形的性质及学生的阅读理解能力．
练习册系列答案
相关题目
如图所示，在Rt△ABC中，∠C=90°，∠B=40°，BC=10，解这个直角三角形（精确到0.1）（sin40°≈0.643，cos40°≈0.766，tan40°≈0.839）
如图，小敏同学想测量一棵大树的高度．她站在B处仰望树顶，测得仰角为30°，再往大树的方向前进4m到点C，测得仰角为60°，已知小敏同学身高（AB）为1.6m，求这棵树的高度（DF）．（结果精确到0.1m，
如图的几何体，从上面看得到的平面图形是（ ）A、 |
B、 |
C、 |
D、 |
如图所示为7×6的正方形网格，点A，B，C在格点上．在图中确定格点D，并画出以A，B，C，D为顶点的四边形计算|1-
|-
的结果为（ ）
| 2 |
(
|
| A、3 | ||
B、2
| ||
| C、1 | ||
D、2
|