题目内容
20．若方程kx2-10x+3=0有一个解x=$\frac{3}{4}$，求k-$\frac{1}{k}$的值．分析 把x的值代入已知方程得到关于k的新方程，通过解新方程来求k的值，则易得所求代数式的值．
解答 解：把x=$\frac{3}{4}$代入kx2-10x+3=0，得
$（\frac{3}{4}）^{2}$k-10×$\frac{3}{4}$+3=0，
解得k=8，
则k-$\frac{1}{k}$=8-$\frac{1}{8}$=$\frac{63}{8}$．
点评 本题考查了一元二次方程的解的定义．一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
10．“十二五”期间是宁波市加快发展现代渔业的重要时期，为适应市场需求，某水产养殖场兴建了标准化高效健康养殖示范区，计划今年养殖梭子蟹和南美白对虾，由于受养殖水面的制约，这两种品种的苗种的总投放量只有50吨，根据经验测算，这两种品种的种苗每投放一顿的先期投资、养殖期间的投资以及产值如表所示：（单位：千元/吨）
（1）要使产值达到1350千克，问梭子蟹和南美白对虾各应养殖多少吨？
（2）若养殖场先期投资不超过360千元，养殖期间的投资不超过290千元，设梭子蟹种苗的投放量为x吨．
①求x的取值范围；
②设这两个品种产出后的总产值为y（千元），试写出y与x之间的函数解析式，当x等于多少时，y有最大值？最大值是多少？
| 品种 | 先期投资 | 养殖期间的投资 | 产值 |
| 梭子蟹 | 9 | 3 | 30 |
| 南美白对虾 | 4 | 10 | 20 |
（2）若养殖场先期投资不超过360千元，养殖期间的投资不超过290千元，设梭子蟹种苗的投放量为x吨．
①求x的取值范围；
②设这两个品种产出后的总产值为y（千元），试写出y与x之间的函数解析式，当x等于多少时，y有最大值？最大值是多少？
11．平面直角坐标系中，把点A（-3，-2）向右沿x轴方向平移5个单位后得到A′，则点A′的坐标是（ ）
| A． | （3，2） | B． | （2，-2） | C． | （-3，2） | D． | （3，-2） |
15．
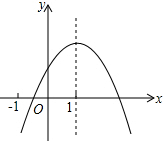如图，二次函数y=ax2+bx+c是一条以x=1为对称轴的抛物线，下列式子成立的是（ ）
如图，二次函数y=ax2+bx+c是一条以x=1为对称轴的抛物线，下列式子成立的是（ ）| A． | abc＞0 | B． | b＜a+c | C． | a+b+c＜0 | D． | 2c＜3b |
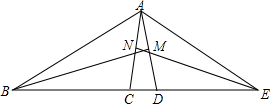如图，已知点B，C，D，E在同一条直线上，BM，EN分别垂直平分AD，AC于M，N．