题目内容
如图所示，一水库迎水坡AB的坡度i=1：2，求坡角α的正弦值sinα
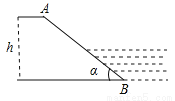
【解析】试题分析：首先过点A作AC⊥BC于点C，设AC=x，根据AC=x，根据坡比可得BC=2x，根据勾股定理求出AB的长度，然后根据正弦的求法得出答案．
试题解析：过A作AC⊥BC于C， ∵AB的坡度i=1：2，
∴tanα=， 设AC=x，BC=2x， 根据勾股定理可得：AB= ，
则sinα=．
名师点拨卷系列答案扎西的爷爷用一段长30m的篱笆围成一个一边靠墙的矩形菜园，墙长为18m，这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少？
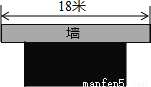
当矩形的长为15m，宽为7.5m时，矩形菜园的面积最大，最大面积为112.5m2
【解析】试题分析：设菜园宽为x，则长为36-2x，由面积公式写出y与x的函数关系式，然后利用二次函数的最值的知识可得出菜园的最大面积，及取得最大面积时矩形的长和宽．
设长为x米，宽为(30-x)/2米-,面积为y米2
当x=15时，y最大=112.5
答：最大面积是112.5米2． 某商场要经营一种新上市的文具，进价为20元，试营销阶段发现：当销售单价是25元时，每天的销售量为250件，销售单价每上涨1元，每天的销售量就减少10件．
(1)写出商场销售这种工具，每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式；
(2)求销售单价为多少元时，该文具每天的销售利润最大；
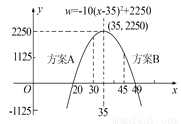
(3)商场的营销部结合上述情况，提出了A、B两种营销方案：
方案A：该文具的销售单价高于进价且不超过30元；
方案B：每天销售量不少于10件，且每件文具的利润至少为25元．
请比较哪种方案的最大利润更高，并说明理由．
（1）w＝－10x2＋700x－10000；
（2）销售单价为35元时，每天销售利润最大，最大利润为2250元；
（3）方案A的最大利润更高，理由见解析.
【解析】试题分析：（1）根据利润=（销售单价-进价）×销售量，列出函数关系式即可；
（2）根据（1）式列出的函数关系式，运用配方法求最大值；
（3）分别求出方案A、B中x的取值范围，然后分别求出A、B方案的最大利润... 二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，若|ax2＋bx＋c|＝k(k≠0)有两个不相等的实数根，则k的取值范围是( )
A. k＜－3 B. k＞－3 C. k＜3 D. k＞3
D
【解析】试题分析：∵当ax2+bx+c≥0，y=ax2+bx+c（a≠0）的图象在x轴上方，
∴此时y=|ax2+bx+c|=ax2+bx+c，
∴此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c（a≠0）在x轴上方部分的图象，
∵当ax2+bx+c＜0时，y=ax2+bx+c（a≠0）的图象在x轴下方，
∴此时y=|ax2+bx+c|=﹣（ax2+b... 若二次函数y＝x2＋bx＋4配方后为y＝(x－2)2＋k，则b、k的值分别为( )
A. 0，5 B. 0，1 C. －4，5 D. －4，0
D
【解析】∵二次函数y＝x2＋bx＋4配方后是y＝（x－2）2＋k
∴a=1， -=2， c=4
∴b=-4
∴ k==1
故选：D. 如图，在坡度为1：3的山坡上种树，要求株距（相邻两树间的水平距离）是6米，则斜坡上相邻两树间的坡面距离是 米（结果保留根号）．
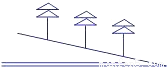
2.
【解析】
试题分析：如图，
Rt△ABC中，∠C=90°，tanA=，AC=6，
∴BC=AC•tanA=6×=2．
根据勾股定理，得：AB=．
即斜坡上相邻两树间的坡面距离是2米． 如图，某水渠的横断面是等腰梯形，已知其斜坡AD和BC的坡度为1：0.6，现测得放水前的水面宽EF为1.2米，当水闸放水后，水渠内水面宽GH为2.1米．求放水后水面上升的高度是（ ）
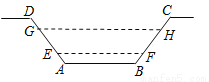
A. 0.55 B. 0.8 C. 0.6 D. 0.75
D
【解析】试题分析：过点E作EM⊥GH，则GM=(2.1-1.2)÷2=0.45米，根据坡度可得：EM=0.45÷0.6=0.75米，故选D． 某厂今年一月份新产品的研发资金为a元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为____．
y＝a(1＋x)2
【解析】试题分析：∵一月份新产品的研发资金为a元，
2月份起，每月新产品的研发资金与上月相比增长率都是x，
∴2月份研发资金为，∴三月份的研发资金为．
故答案为： ． 把多项式(m+1)（m-1）+（m-1）分解因式，一个因式是（m-1）,则另一个因式是（ ）
A. m+1 B. 2m C. 2 D. m+2
D
【解析】∵(m+1)（m-1）+（m-1）=（m-1）（m+1+1）=（m-1）（m+2），
∴另一个因式是（m+2）.
故选D.