题目内容
20. 如图,在△ABC中,BC=AC,∠A=90°,AC=7cm,AD是∠BAC的平分线,交BC于D,DE⊥AB于E,CD=3cm,求△DEB的周长.
如图,在△ABC中,BC=AC,∠A=90°,AC=7cm,AD是∠BAC的平分线,交BC于D,DE⊥AB于E,CD=3cm,求△DEB的周长.
分析 根据等腰直角三角形的性质得到∠B=45°,根据角平分线的性质得到DE=DC=3cm,根据等腰直角三角形的性质和三角形的周长公式计算即可.
解答 解:∵BC=AC,∠A=90°,
∴∠CAB=∠B=45°,
∵AD是∠BAC的平分线,∠A=90°,DE⊥AB,
∴DE=DC=3cm,
∵∠B=45°,
∴ED=EB=3cm,BD=3$\sqrt{2}$cm,
∴△DEB的周长=DE+BE+BD=(6+3$\sqrt{2}$)cm.
点评 本题考查的是角平分线的性质和等腰直角三角形的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
9.在今年的“希望工程”捐款活动中,某班级一小组7名同学积极捐出自己的零花锇,奉献自己的爱心,他们捐款的数额分别是(单位:元)5O、20、5O、30、25、50、55,这组数据的众数和中位数分别是( )
| A. | 50元,30元 | B. | 50元,40元 | C. | 50元,50元 | D. | 55元,50元 |
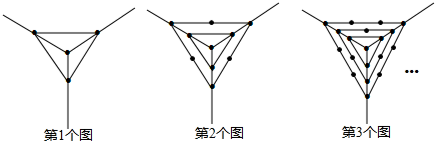
10.观察下列一组图形中黑点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第16个图中共有点的个数是( )

| A. | 408 | B. | 409 | C. | 361 | D. | 360 |
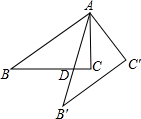 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕点A逆时针旋转得到△AB′C′,AB′与BC相交于点D,当B′C′∥AB时,CD=$\frac{7}{8}$.
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将△ABC绕点A逆时针旋转得到△AB′C′,AB′与BC相交于点D,当B′C′∥AB时,CD=$\frac{7}{8}$.