题目内容
20.在以0为原点的平面直角坐标系中,Q是反比例函数y=$\frac{k}{x}$图象上一点,以Q为圆心、CQ为半径的圆与x,y轴分别交于点M,N,则MO•NO=4|k|.分析 设点Q的坐标为(x,y),由Q是反比例函数y=$\frac{k}{x}$图象上一点可得xy=k.过点Q作QE⊥OM于E,作QF⊥ON于F,如图,根据垂径定理可得OE=EM=$\frac{1}{2}$OM=|x|,OF=FN=$\frac{1}{2}$ON=|y|,从而可求出OM•ON.
解答 解:设点Q的坐标为(x,y),
∵Q是反比例函数y=$\frac{k}{x}$图象上一点,
∴xy=k.
过点Q作QE⊥OM于E,作QF⊥ON于F,如图,
根据垂径定理可得OE=EM=$\frac{1}{2}$OM=|x|,OF=FN=$\frac{1}{2}$ON=|y|.
∴OM=2|x|,ON=2|y|,
∴OM•ON=4|xy|=4|k|.
故答案为4|k|.
点评 本题主要考查了反比例函数图象上点的坐标特征、垂径定理等知识,需要注意的是,纵、横坐标符号不确定时,要用纵、横坐标的绝对值表示线段长度.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
15.若a<b,则|b-a+1|-|a-b|等于( )
| A. | -1 | B. | 1 | C. | -2a+2b+1 | D. | 2a-2b-1 |
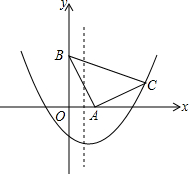 如图,在平面直角坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=x2+bx-2过点C.求抛物线的解析式.
如图,在平面直角坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线y=x2+bx-2过点C.求抛物线的解析式.