题目内容
5.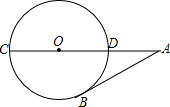 如图,CD是⊙O的直径,点A在CD的延长线上,AB切⊙O于点B,若∠A=30°,OA=10,则AB=5$\sqrt{3}$.
如图,CD是⊙O的直径,点A在CD的延长线上,AB切⊙O于点B,若∠A=30°,OA=10,则AB=5$\sqrt{3}$.
分析 连接BO,根据切线性质得出∠OBA=90°,根据含30度角的直角三角形性质求出OB=$\frac{1}{2}$OA,代入可求出OB的长,再利用勾股定理即可求出AB的长.
解答 解:
连接OB,
∵AB切⊙O于B,
∴∠OBA=90°,
∵∠A=30°,OA=10,
∴OB=$\frac{1}{2}$OA=5,
∴AB=$\sqrt{A{O}^{2}-O{B}^{2}}$=5$\sqrt{3}$
故答案为:5$\sqrt{3}$.
点评 本题考查了切线性质和含30度角的直角三角形性质的应用以及勾股定理的运用,解题的关键是得出OB=$\frac{1}{2}$OA.

练习册系列答案
相关题目
17.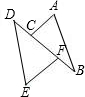 如图,AB∥ED,CD=BF,若△ABC≌△EDF,则还需要补充的条件可以是( )
如图,AB∥ED,CD=BF,若△ABC≌△EDF,则还需要补充的条件可以是( )
 如图,AB∥ED,CD=BF,若△ABC≌△EDF,则还需要补充的条件可以是( )
如图,AB∥ED,CD=BF,若△ABC≌△EDF,则还需要补充的条件可以是( )| A. | AC=EF | B. | BC=DF | C. | AB=DE | D. | ∠B=∠E |
 如图是一个由两个小正方体和一个圆锥组成的几何体,它的左视图是( )
如图是一个由两个小正方体和一个圆锥组成的几何体,它的左视图是( )



 如图,对?ABCD对角线交点O的直线分别交AB的延长线于点E,交CD的延长线于点F,若AB=4,AE=6,则DF的长等于2.
如图,对?ABCD对角线交点O的直线分别交AB的延长线于点E,交CD的延长线于点F,若AB=4,AE=6,则DF的长等于2. 如图,菱形ABCD的两条对角线分别长4和6,点P是对角线AC上的一个动点,点M,N分别是边AB,BC的中点,则PM+PN的最小值是$\sqrt{13}$.
如图,菱形ABCD的两条对角线分别长4和6,点P是对角线AC上的一个动点,点M,N分别是边AB,BC的中点,则PM+PN的最小值是$\sqrt{13}$.