题目内容
20. 如图,菱形ABCD的两条对角线分别长4和6,点P是对角线AC上的一个动点,点M,N分别是边AB,BC的中点,则PM+PN的最小值是$\sqrt{13}$.
如图,菱形ABCD的两条对角线分别长4和6,点P是对角线AC上的一个动点,点M,N分别是边AB,BC的中点,则PM+PN的最小值是$\sqrt{13}$.
分析 要求PM+PN的最小值,PM、PN不能直接求,可作M关于AC的对称点E,再连接EN,利用菱形的性质计算出EN的长,EN就是PM+PN的最小值.
解答 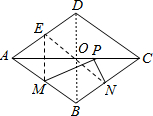 解:如图:作ME⊥AC交AD于E,连接EN、BD,则EN就是PM+PN的最小值,
解:如图:作ME⊥AC交AD于E,连接EN、BD,则EN就是PM+PN的最小值,
∵四边形ABCD是菱形,
∴AB=BC=AD=DC,AC⊥BD,AO=$\frac{1}{2}$AC=3,BO=$\frac{1}{2}$BD=3,
∵M、N分别是AB、BC的中点,
∴BN=BM=AM,
∵ME⊥AC交AD于E,
∴AE=AM,
∴AE=BN,AE∥BN,
∴四边形ABNE是平行四边形,
∴EN=AB,EN∥AB,
而由题意可知,可得AB=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
∴EN=AB=$\sqrt{13}$,
∴PM+PN的最小值为$\sqrt{13}$.
故答案为:$\sqrt{13}$.
点评 此题主要考查菱形的性质和轴对称及平行四边形的判定等知识的综合应用.关键是掌握菱形是轴对称图形,菱形对角线互相垂直且平分.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.已知一组数据:-2,5,2,-1,0,4,则这组数据的中位数是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
 数学实践活动小组实地测量山峰与山下广场的相对高度AB,器测量步骤如下:
数学实践活动小组实地测量山峰与山下广场的相对高度AB,器测量步骤如下:



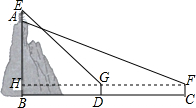
 如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,点M,N分别在边AB,BC上,点E,F分别为MN,DN的中点,连接EF,则EF长度的最大值为3.
如图,在四边形ABCD中,∠A=90°,AB=3$\sqrt{3}$,AD=3,点M,N分别在边AB,BC上,点E,F分别为MN,DN的中点,连接EF,则EF长度的最大值为3.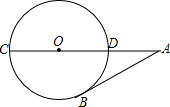 如图,CD是⊙O的直径,点A在CD的延长线上,AB切⊙O于点B,若∠A=30°,OA=10,则AB=5$\sqrt{3}$.
如图,CD是⊙O的直径,点A在CD的延长线上,AB切⊙O于点B,若∠A=30°,OA=10,则AB=5$\sqrt{3}$.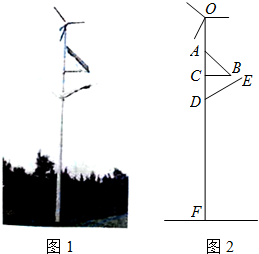 如图1,某利用风能、太阳能发电的风光互补环保路灯的灯杆顶端装有风力发电机,中间装有太阳能板,下端装有路灯.该系统工作过程中某一时刻的截面图如图2,已知太阳能板的支架BC垂直于灯杆OF,路灯顶端E距离地面6米,DE=1.8米,∠CDE=60°.且根据我市的地理位置设定太阳能板AB的倾斜角为43°,AB=1.5米,CD=1米.为保证长为1米的风力发电机叶片无障碍安全旋转,叶片与太阳能板顶端A的最近距离不少于0.5米,求灯杆OF至少要多高(利用科学计算器可求得sin43°≈0.6820,cos43°≈0.7314,tan43°≈0.9325,结果保留两位小数)?
如图1,某利用风能、太阳能发电的风光互补环保路灯的灯杆顶端装有风力发电机,中间装有太阳能板,下端装有路灯.该系统工作过程中某一时刻的截面图如图2,已知太阳能板的支架BC垂直于灯杆OF,路灯顶端E距离地面6米,DE=1.8米,∠CDE=60°.且根据我市的地理位置设定太阳能板AB的倾斜角为43°,AB=1.5米,CD=1米.为保证长为1米的风力发电机叶片无障碍安全旋转,叶片与太阳能板顶端A的最近距离不少于0.5米,求灯杆OF至少要多高(利用科学计算器可求得sin43°≈0.6820,cos43°≈0.7314,tan43°≈0.9325,结果保留两位小数)?