题目内容
 如图,AB为⊙O的直径,BC为弦,且∠ABC=30°,点P、Q分别是AB、BC上一点,且PQ+PC=5恒成立,则直径AB的最大值为
如图,AB为⊙O的直径,BC为弦,且∠ABC=30°,点P、Q分别是AB、BC上一点,且PQ+PC=5恒成立,则直径AB的最大值为考点:圆的综合题
专题:
分析:过点C作AB的对称点D,连接DC、DB、DA、DQ,过点D作DH⊥BC于H,交AB于G,连接GC,根据对称性可得PD=PC,∠DBA=∠CBA=30°,从而有∠DBC=60°,由圆的对称性可得点D在⊙O上,则有∠BDA=90°,然后利用三角函数可得BA=
DH,根据点到直线之间垂线段最短可得DH≤DQ,根据两点之间线段最短可得DQ≤PD+PQ=PC+PQ=5,则有DH≤5.,从而可求出直径AB的最大值.
| 4 |
| 3 |
解答: 解:过点C作AB的对称点D,连接DC、DB、DA、DQ,
解:过点C作AB的对称点D,连接DC、DB、DA、DQ,
过点D作DH⊥BC于H,交AB于G,连接GC,如图所示,
则有PD=PC,∠DBA=∠CBA=30°,
则有∠DBC=60°.
由圆的对称性可得点D在⊙O上,则有∠BDA=90°.
在Rt△ADB中,cos∠DBA=
=
.
在Rt△BHD中,sin∠DBH=
=
.
则有
=
•
=
•
=
,
所以BA=
DH.
根据点到直线之间垂线段最短可得DH≤DQ,
根据两点之间线段最短可得DQ≤PD+PQ=PC+PQ=5,
所以DH≤5.
∴BA=
DH≤
.
∴直径AB的最大值为
.
故答案为:
.
 解:过点C作AB的对称点D,连接DC、DB、DA、DQ,
解:过点C作AB的对称点D,连接DC、DB、DA、DQ,过点D作DH⊥BC于H,交AB于G,连接GC,如图所示,
则有PD=PC,∠DBA=∠CBA=30°,
则有∠DBC=60°.
由圆的对称性可得点D在⊙O上,则有∠BDA=90°.
在Rt△ADB中,cos∠DBA=
| BD |
| BA |
| ||
| 2 |
在Rt△BHD中,sin∠DBH=
| DH |
| BD |
| ||
| 2 |
则有
| DH |
| BA |
| BD |
| BA |
| DH |
| BD |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 4 |
所以BA=
| 4 |
| 3 |
根据点到直线之间垂线段最短可得DH≤DQ,
根据两点之间线段最短可得DQ≤PD+PQ=PC+PQ=5,
所以DH≤5.
∴BA=
| 4 |
| 3 |
| 20 |
| 3 |
∴直径AB的最大值为
| 20 |
| 3 |
故答案为:
| 20 |
| 3 |
点评:本题主要考查了轴对称的性质、三角函数、点到直线之间垂线段最短、两点之间线段最短等知识,证到BA=
DH及DH≤5是解决本题的关键.
| 4 |
| 3 |

练习册系列答案
相关题目
 如图,AD为△ABC的中线,BE⊥AD于E,CF⊥AD于F,求证:DE=DF.
如图,AD为△ABC的中线,BE⊥AD于E,CF⊥AD于F,求证:DE=DF.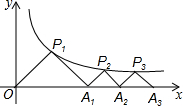 如图所示,P1(x1,y1)、P2(x2,y2),…,Pn(xn,yn)在函数y=
如图所示,P1(x1,y1)、P2(x2,y2),…,Pn(xn,yn)在函数y=