题目内容
10．
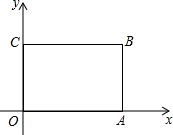如图，矩形OABC的顶点坐标分别为O（0，0）、A（6，0）、B（6，4）、C（0，4），画出以点O为位似中心，矩形OABC的位似图形O′A′B′C′，使它的面积等于矩形OABC面积的$\frac{1}{4}$，并分别写出点A′，B′，C′的坐标．
分析 首先由画出以点O为位似中心，矩形OABC的位似图形O′A′B′C′，使它的面积等于矩形OABC面积的$\frac{1}{4}$，可求得其位似比，继而求得点A′，B′，C′的坐标，则可画出图形．
解答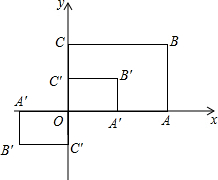 
解：∵矩形O′A′B′C′的面积等于矩形OABC面积的$\frac{1}{4}$，且矩形O′A′B′C′与矩形OABC位似，
∴位似比为1：2，
∵矩形OABC的顶点坐标分别为O（0，0）、A（6，0）、B（6，4）、C（0，4），
∴矩形O′A′B′C′的顶点坐标分别为：O（0，0）、A′（3，0）、B′（3，2）、C′（0，2）或O（0，0）、A′（-3，0）、B′（-3，-2）、C′（0，-2）．
∴点A′，B′，C′的坐标分别为：A′（3，0）、B′（3，2）、C′（0，2）或A′（-3，0）、B′（-3，-2）、C′（0，-2）．
点评 此题考查了位似变换．注意理解位似是相似的特殊情况，由面积比求得其位似比是关键．
练习册系列答案
阅读快车系列答案
相关题目
20．图中间问号处的数应为（ ）
| A． | 22 | B． | 23 | C． | 24 | D． | 25 |
如图，点D，E在线段BC上，且△ABC是等边三角形，当DB，BC，CE满足怎样的关系时，△ADB∽△EAC，并加以证明．
如图，已知△ABC中，∠B=90°，AB=8cm，BC=6cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．