题目内容
1. 如图,点D,E在线段BC上,且△ABC是等边三角形,当DB,BC,CE满足怎样的关系时,△ADB∽△EAC,并加以证明.
如图,点D,E在线段BC上,且△ABC是等边三角形,当DB,BC,CE满足怎样的关系时,△ADB∽△EAC,并加以证明.
分析 先根据等边三角形的性质得AB=BC=AC,∠ABC=∠ACB=60°,则利用邻补角的定义可得∠ABD=∠ACE,于是根据两组对应边的比相等且夹角对应相等的两个三角形相似,当$\frac{AB}{EC}$=$\frac{DB}{AC}$时,可判断△ADB∽△EAC,然后利用等线段代换即可得到DB,BC,CE的关系.
解答 解:当DB,BC,CE满足BC2=DB•CE时,△ADB∽△EAC,
∵△ABC是等边三角形,
∴AB=BC=AC,∠ABC=∠ACB=60°,
∴∠ABD=∠ACE=120°,
∴当$\frac{AB}{EC}$=$\frac{DB}{AC}$时,△ADB∽△EAC,
即AB•AC=DB•EC,
而AB=BC=AC,
即有BC2=DB•CE.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.也考查了等边三角形的性质.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
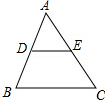 如图,在△ABC中,已知DE∥BC,AD=5,DB=3,BC=10,求:
如图,在△ABC中,已知DE∥BC,AD=5,DB=3,BC=10,求: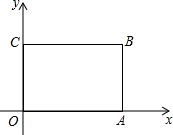 如图,矩形OABC的顶点坐标分别为O(0,0)、A(6,0)、B(6,4)、C(0,4),画出以点O为位似中心,矩形OABC的位似图形O′A′B′C′,使它的面积等于矩形OABC面积的$\frac{1}{4}$,并分别写出点A′,B′,C′的坐标.
如图,矩形OABC的顶点坐标分别为O(0,0)、A(6,0)、B(6,4)、C(0,4),画出以点O为位似中心,矩形OABC的位似图形O′A′B′C′,使它的面积等于矩形OABC面积的$\frac{1}{4}$,并分别写出点A′,B′,C′的坐标.