题目内容
5.已知-3xm-2ny-n+2与$\frac{1}{5}$x2y-1+m是同类项,求(m-2n)2-5(m+n)-2(m-2n)2+m+n的值.分析 利用同类项定义求出m与n的值,原式合并后代入计算即可求出值.
解答 解:∵-3xm-2ny-n+2与$\frac{1}{5}$x2y-1+m是同类项,
∴$\left\{\begin{array}{l}{m-2n=2}\\{-n+2=-1+m}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=\frac{8}{3}}\\{n=\frac{1}{3}}\end{array}\right.$,即m+n=3,m-2n=2,
则原式=-(m-2n)2-4(m+n)=-4-12=-16.
点评 此题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
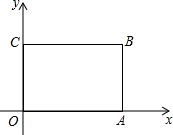 如图,矩形OABC的顶点坐标分别为O(0,0)、A(6,0)、B(6,4)、C(0,4),画出以点O为位似中心,矩形OABC的位似图形O′A′B′C′,使它的面积等于矩形OABC面积的$\frac{1}{4}$,并分别写出点A′,B′,C′的坐标.
如图,矩形OABC的顶点坐标分别为O(0,0)、A(6,0)、B(6,4)、C(0,4),画出以点O为位似中心,矩形OABC的位似图形O′A′B′C′,使它的面积等于矩形OABC面积的$\frac{1}{4}$,并分别写出点A′,B′,C′的坐标. 已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,求作$\overrightarrow{a}$-$\overrightarrow{b}$.
已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,求作$\overrightarrow{a}$-$\overrightarrow{b}$.