题目内容
定义新运算可以做为一类数学问题,如:x,y表示两个数,规定新运算“*”及“△”如下:x*y=mx+ny,
x△y=kxy,其中m,n,k均为非零自然数.已知1*2=5,(2*3)△4=64,那么(1△2)*3= .
x△y=kxy,其中m,n,k均为非零自然数.已知1*2=5,(2*3)△4=64,那么(1△2)*3=
考点:有理数的混合运算
专题:新定义
分析:已知两式利用题中的新定义化简,整理得到两个关系式,根据m,n,k均为非零自然数,由①求出m与n的值,进而求出k的值,再利用题中的新定义求出所求式子的值即可.
解答:解:根据题意得:1*2=m+2n=5①,(2*3)△4=4k(2m+3n)=64,即k(2m+3n)=16②,
∵x、y、m、n、k均为自然数
∴由①解得:m=1,n=2或m=3,n=1;
分别代入②,得,k=2或无解.
∴m=1,n=2,k=2,
则(1△2)*3=4*3=4+6=10,
故答案为:10
∵x、y、m、n、k均为自然数
∴由①解得:m=1,n=2或m=3,n=1;
分别代入②,得,k=2或无解.
∴m=1,n=2,k=2,
则(1△2)*3=4*3=4+6=10,
故答案为:10
点评:此题考查了有理数的混合运算,弄清题中的新定义是解本题的关键.

练习册系列答案
相关题目
点A,B都在半径为5的圆O上,AB=6,则O到线段AB的长度是( )
| A、11 | B、6 | C、5 | D、4 |
下列各组式子是同类项的是( )
| A、2ab2与-ba2 |
| B、-mn与mn |
| C、5x2y与-2xy2 |
| D、3a与3ab |
 如图,在梯形ABCD中,AD∥BC,∠B=90°,E是AB的中点,且DC=AD+BC,则下列结论中错误的有( )
如图,在梯形ABCD中,AD∥BC,∠B=90°,E是AB的中点,且DC=AD+BC,则下列结论中错误的有( )| A、DE平分∠ADC |
| B、△DEC是直角三角形 |
| C、点E到DC的距离为AB长的一半 |
| D、△DEC的面积为△ADE面积的2倍 |
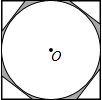 已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )
已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )A、32
| ||
B、
| ||
| C、1 | ||
| D、16-4π |
 如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/s;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).
如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/s;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5). 如图,矩形OABC的顶点C、A分别在x轴和y轴上,点B的坐标为(4,3),双曲线y=
如图,矩形OABC的顶点C、A分别在x轴和y轴上,点B的坐标为(4,3),双曲线y= 如图,以O为圆心,任意长为半径画弧,与射线OM相交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于( )
如图,以O为圆心,任意长为半径画弧,与射线OM相交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于( )