题目内容
18.如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.(1)若(x-2)(mx+n)=0是倍根方程,求证:4m2+5mn+n2=0;
(2)若点(p,q)在函数y=2x+2的图象上,说明关于x的方程(q-2p)x2+3x+1=0是倍根方程.
分析 (1)根据(x-2)(mx+n)=0是倍根方程,且x1=2,x2=-$\frac{n}{m}$得到$\frac{n}{m}$=-1,或$\frac{n}{m}$=-4,从而得到m+n=0,4m+n=0,进而得到4m2+5mn+n2=(4m+n)(m+n)=0正确;
(2)把(p,q)代入y=2x+2得q-2p=2,可得原方程为2x2+3x+1=0,解方程即可判断.
解答 解:(1))∵(x-2)(mx+n)=0是倍根方程,且x1=2,x2=-$\frac{n}{m}$,
∴$\frac{n}{m}$=-1或$\frac{n}{m}$=-4,
∴m+n=0,4m+n=0,
∵4m2+5mn+n2=(4m+n)(m+n)=0;
(2)把(p,q)代入y=2x+2,得:q=2p+2,
则q-2p=2,
原方程为2x2+3x+1=0,
解得:x1=-$\frac{1}{2}$,x2=-1,
∵x2=2x1,
∴它是倍根方程.
点评 本题考查了一元二次方程的解、一次函数函数图形上点的坐标特征,正确的理解“倍根方程”的定义是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.某商场用18万购进A、B两种电器,销售完共获利5万元,其进价和售价如表:
(1)该商场购进A、B两种电器各多少台?
(2)商场第二次以原价购进A、B两种电器,购进A电器的台数不变,B电器的台数是第一次的$\frac{1}{2}$;B种电器按原价出售,而A种电器打折销售.若两种电器销售完毕,要使第二次经营获利不少于25000元,A种电器最低售价为每台多少元?
| A | B | |
| 进价(元/台) | 500 | 600 |
| 售价(元/台) | 600 | 790 |
(2)商场第二次以原价购进A、B两种电器,购进A电器的台数不变,B电器的台数是第一次的$\frac{1}{2}$;B种电器按原价出售,而A种电器打折销售.若两种电器销售完毕,要使第二次经营获利不少于25000元,A种电器最低售价为每台多少元?
10.一个圆锥的侧面展开图形是半径为8cm,圆心角为120°的扇形,则此圆锥的底面半径为( )
| A. | $\frac{8}{3}$ cm | B. | $\frac{16}{3}$ cm | C. | 3cm | D. | $\frac{4}{3}$ cm |
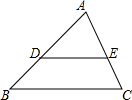 在△ABC 中,$\frac{AD}{DB}$=$\frac{AE}{EC}$,AB=8,AE=4,EC=2,求AD的长.
在△ABC 中,$\frac{AD}{DB}$=$\frac{AE}{EC}$,AB=8,AE=4,EC=2,求AD的长. 如图所示,在Rt△ABC中,∠B=90°,AC=100cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤25).过点D作DF⊥BC于点F,连接DE,EF.
如图所示,在Rt△ABC中,∠B=90°,AC=100cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤25).过点D作DF⊥BC于点F,连接DE,EF.